Mean of Standard Normal Distribution: Central Value

_{September 20, 2023 by JoyAnswer.org, Category : Statistics}

What is the mean of standard normal distribution? Explore the concept of the mean in a standard normal distribution, which represents the central value in a bell-shaped curve of standardized data.

What is the mean of standard normal distribution?

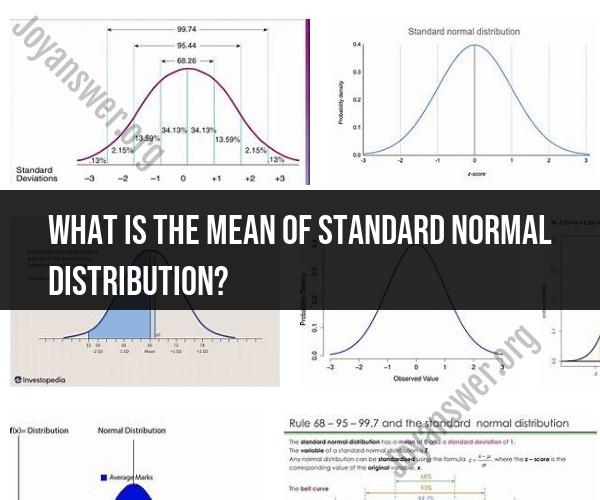
The standard normal distribution, also known as the Z-distribution, is a specific type of normal distribution with a mean (average) of 0 and a standard deviation of 1. In this distribution, the mean (μ) is always 0, and the standard deviation (σ) is always 1. This means that the central value, or the expected value, of the standard normal distribution is 0.

In mathematical notation, the probability density function (PDF) of the standard normal distribution is given by:

f(x) = (1 / √(2π)) * e^(-x^2/2)

Where:

f(x) is the probability density at a given value x.
π is the mathematical constant pi (approximately 3.14159).
e is the mathematical constant approximately equal to 2.71828.

The mean of this distribution, μ, is 0, indicating that the peak of the bell-shaped curve is centered at 0 on the x-axis. The standard deviation, σ, is 1, which determines the spread or width of the curve.

In practical terms, the standard normal distribution is often used as a reference distribution in statistics and probability theory. It serves as a basis for calculating z-scores (standard scores) and for making statistical inferences about other normal distributions by standardizing them to have a mean of 0 and a standard deviation of 1.

The mean of the standard normal distribution is 0, which means that the data is evenly distributed on either side of the mean. The standard normal distribution is a special case of the normal distribution, where the mean is 0 and the standard deviation is 1.

The mean of the standard normal distribution is a central measure of tendency, which means that it represents the central value of the distribution. The other two central measures of tendency are the median and the mode. The median is the middle value of the distribution, and the mode is the most frequent value of the distribution.

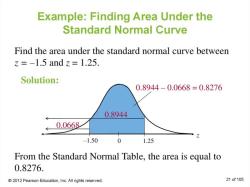
The mean of the standard normal distribution is significant in statistics because it is used to calculate the z-scores of data points. A z-score is a measure of how many standard deviations a data point is away from the mean. Z-scores can be used to compare different data sets and to identify outliers.

For example, a z-score of 1 means that a data point is one standard deviation above the mean. A z-score of -2 means that a data point is two standard deviations below the mean.

The mean of the standard normal distribution is also used in a variety of statistical tests, such as the t-test and the chi-squared test. These tests are used to compare different groups of data and to determine whether there is a statistically significant difference between the groups.

Here are some examples of how the mean of the standard normal distribution is used in real-world applications:

Education: The mean of the standard normal distribution is used in education to compare the performance of different students and to identify students who are struggling or who are excelling in a particular subject.
Business: The mean of the standard normal distribution is used in business to predict customer demand, to set sales goals, and to make investment decisions.
Healthcare: The mean of the standard normal distribution is used in healthcare to diagnose diseases, to predict patient outcomes, and to develop new treatments.

The mean of the standard normal distribution is a powerful tool that can be used in a wide variety of fields. By understanding the mean of the standard normal distribution, we can better understand the world around us and make better decisions.