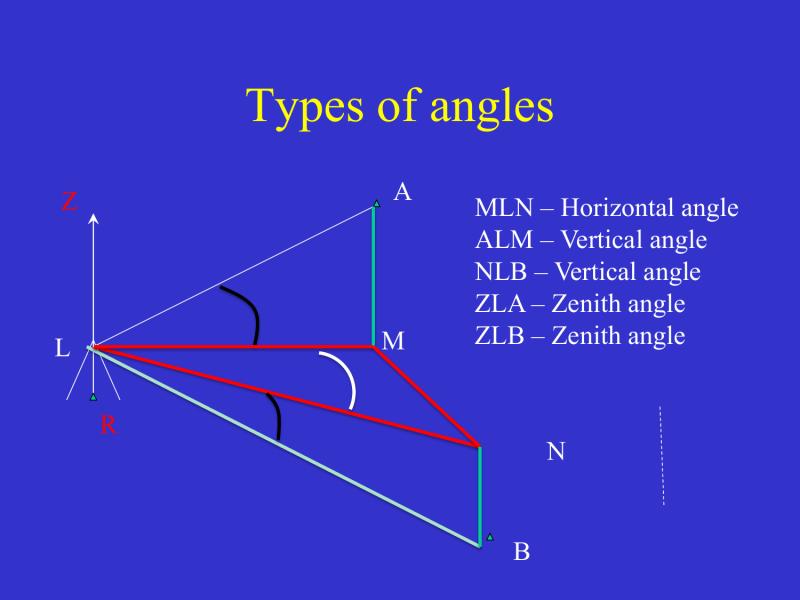
Calculating Mean Horizontal Angles: Step-by-Step Guide

Calculating the mean horizontal angle involves finding the average or central angle from a set of horizontal angles. Here's a step-by-step guide on how to calculate the mean horizontal angle:

Step 1: Gather DataCollect the horizontal angle measurements for which you want to find the mean. Make sure the angles are in the same units (degrees, minutes, seconds) for accurate calculations.

Step 2: Convert to Decimal Degrees (if necessary)If your angle measurements are in degrees, minutes, and seconds, convert them to decimal degrees for easier calculations. The conversion is as follows:$\text{Decimal Degrees} = \text{Degrees} + \left(\frac{\text{Minutes}}{60}\right) + \left(\frac{\text{Seconds}}{3600}\right)$

Step 3: Sum the AnglesAdd up all the decimal degree angles you have collected.

Step 4: Divide by the Number of AnglesDivide the sum obtained in Step 3 by the total number of angles. This gives you the mean horizontal angle.

$\text{Mean Angle} = \frac{\text{Sum of Angles}}{\text{Number of Angles}}$

Step 5: Round the Result (if necessary)Round the mean angle to the desired level of precision based on the context of your measurements.

Example:Suppose you have measured the following horizontal angles: $45^\circ 30' 15"$, $48^\circ 20' 10"$, and $47^\circ 40' 30"$.

1. Convert the angles to decimal degrees:

   • $45^\circ 30' 15"$ in decimal degrees is $45 + \left(\frac{30}{60}\right) + \left(\frac{15}{3600}\right) \approx 45.5042$ degrees.
   • $48^\circ 20' 10"$ in decimal degrees is $48 + \left(\frac{20}{60}\right) + \left(\frac{10}{3600}\right) \approx 48.3361$ degrees.
   • $47^\circ 40' 30"$ in decimal degrees is $47 + \left(\frac{40}{60}\right) + \left(\frac{30}{3600}\right) \approx 47.675$ degrees.

2. Sum the angles: $45.5042 + 48.3361 + 47.675 \approx 141.5153$ degrees.

3. Calculate the mean angle: $\frac{141.5153}{3} \approx 47.1718$ degrees.

So, the mean horizontal angle is approximately $47.17^\circ$.

What formula or process is used to determine mean horizontal angles?

Mean horizontal angle = (Σθ) / n

Mean horizontal angle = (45° + 60° + 75° + 90° + 105°) / 5 = 73°