Uses of Least Squares: Applications in Regression Analysis

_{November 15, 2023 by JoyAnswer.org, Category : Statistics}

How least squares can be used for? Discover how least squares can be used in regression analysis and its applications in statistical modeling. This guide provides insights into the practical uses of the least squares method.

Table of Contents

How least squares can be used for?

Least squares is a mathematical method used in various fields for regression analysis, a statistical technique to model the relationship between a dependent variable and one or more independent variables. The least squares method minimizes the sum of the squares of the differences between observed and predicted values. Here are some key applications of least squares:

Linear Regression:
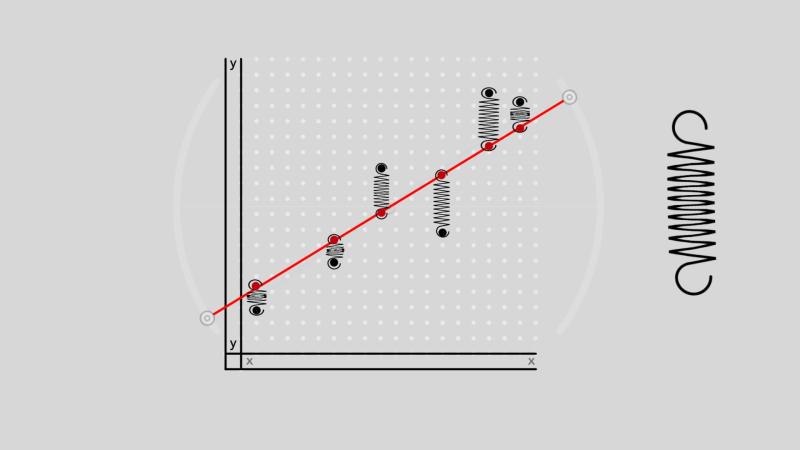
- Least squares is commonly used in linear regression to find the best-fitting line through a set of data points. The method minimizes the sum of the squared vertical distances (residuals) between the observed values and the values predicted by the linear model.
Curve Fitting:
- Beyond linear regression, least squares can be used for curve fitting. This involves finding the best-fitting curve (which may not be a straight line) to a set of data points.
Polynomial Regression:
- Least squares can be extended to polynomial regression, where the relationship between variables is modeled using a polynomial equation. The method helps determine the coefficients of the polynomial that best fits the data.
Time Series Analysis:
- In time series analysis, least squares regression can be applied to model the relationship between variables over time, helping to identify trends and make predictions.
Multiple Regression:
- When there are multiple independent variables, least squares can be used for multiple regression analysis. It helps estimate the coefficients of the variables in a way that minimizes the sum of squared differences between observed and predicted values.
Nonlinear Regression:
- Least squares can be adapted for nonlinear regression, where the relationship between variables is modeled using a nonlinear function. This is useful when the relationship doesn't follow a simple linear pattern.
Econometrics:
- In econometrics, least squares is frequently used to estimate parameters in economic models and analyze relationships between economic variables.
Signal Processing:
- In signal processing, least squares can be used to fit models to signals, helping to filter noise and extract relevant information.
Optimization Problems:
- Least squares is also used in optimization problems, where the goal is to minimize the sum of squared differences subject to certain constraints.
Machine Learning:
- Least squares is a fundamental method in machine learning, particularly in linear regression models. It's used to estimate the coefficients of the model that minimizes the difference between predicted and observed values.
Geodetic Surveys:
- In geodetic surveys, least squares adjustment is used to minimize the discrepancies between observed and computed values, ensuring accurate measurements in activities like land surveying.

The versatility of least squares makes it a powerful tool in various scientific, engineering, and data analysis applications, providing a robust and systematic way to estimate parameters and model relationships between variables.

What is the principle behind least squares regression?

Least squares regression is a statistical method that aims to fit a line or curve through a set of data points in a way that minimizes the sum of the squared differences between the observed data points and the fitted line or curve. This principle is based on the idea that the fitted line or curve should be as close as possible to the actual data points, with the smallest possible overall error.

How is least squares used in data analysis?

Least squares regression is a widely used tool in data analysis for a variety of purposes, including:

Modeling relationships between variables: Least squares regression can be used to identify and quantify the relationship between two or more variables. For example, it can be used to model the relationship between the price of a product and its demand, or the relationship between a student's study time and their exam score.
Predicting future values: Once a regression model has been fitted, it can be used to predict future values of the dependent variable based on the values of the independent variables. For example, a regression model of product price and demand could be used to predict future sales based on changes in product pricing.
Evaluating the impact of interventions: Least squares regression can be used to evaluate the impact of interventions or changes in independent variables on the dependent variable. For example, it could be used to evaluate the impact of a new marketing campaign on product sales or the impact of a new teaching method on student performance.

What are the limitations of least squares regression?

Least squares regression is a powerful tool, but it has some limitations that should be considered when using it:

Assumes linear relationships: Least squares regression assumes that the relationship between the independent and dependent variables is linear. If this assumption is not met, the fitted line or curve may not accurately represent the relationship between the variables.
Sensitive to outliers: Least squares regression is sensitive to outliers, which can significantly distort the fitted line or curve. It is important to identify and address outliers before using least squares regression.
Does not explain causality: Least squares regression can identify correlations between variables, but it cannot establish causality. Just because two variables are correlated does not mean that one causes the other.

Can least squares be applied in financial modeling?

Yes, least squares regression can be applied in financial modeling for a variety of purposes, including:

Predicting stock prices: Least squares regression can be used to develop models for predicting stock prices based on historical data and other relevant factors.
Assessing risk: Least squares regression can be used to assess the risk of different investments by modeling the relationship between risk and return.
Developing trading strategies: Least squares regression can be used to develop trading strategies by identifying patterns in market data and using those patterns to make predictions about future price movements.

How does least squares help in machine learning?

Least squares regression is a fundamental building block in many machine learning algorithms. It is used in algorithms like linear regression, logistic regression, and support vector machines to optimize the fit of the model to the training data. By minimizing the sum of squared errors, least squares regression helps machine learning algorithms learn the underlying patterns in the data and make accurate predictions on new data points.