Unpacking the 90% Confidence Level: Statistical Significance Explained

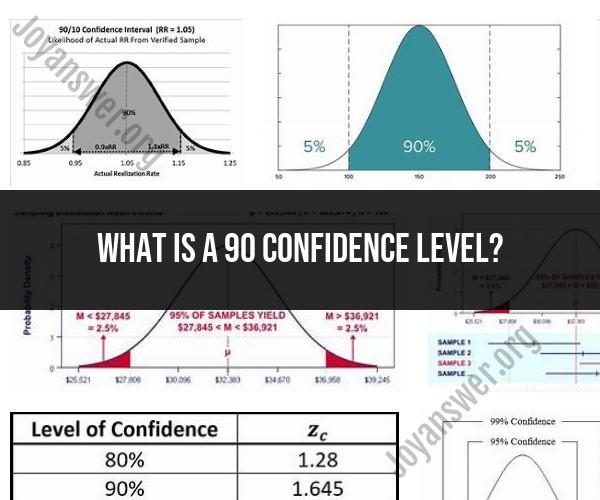
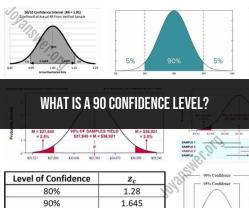
A 90% confidence level is a statistical measure that represents the degree of confidence or certainty that a calculated confidence interval contains the true population parameter. In other words, when you calculate a 90% confidence interval from a sample of data, you can interpret it as follows:

"If we were to take many random samples from the same population and calculate a confidence interval for each sample, we would expect approximately 90% of those intervals to contain the true population parameter."

Here's how a 90% confidence level is typically used in statistics:

1. Sample Data: You start with a sample of data collected from a population. This sample is often used to estimate a population parameter, such as the population mean, population proportion, or population variance.

2. Confidence Interval Calculation: Using statistical methods, you calculate a confidence interval around your sample estimate. The width of the interval depends on factors like the sample size, the level of confidence (in this case, 90%), and the variability in the data.

3. Interpretation: The resulting confidence interval provides a range of values within which you are reasonably confident the true population parameter lies. In the case of a 90% confidence interval, you are saying that you have 90% confidence that the true parameter falls within the interval.

4. Probability of Containment: It's important to understand that the 90% confidence level does not mean that there is a 90% probability that the true parameter falls within the specific interval you calculated. Instead, it means that if you were to conduct many similar experiments and calculate 90% confidence intervals for each, approximately 90% of those intervals would contain the true parameter.

5. Margin of Error: The width of the confidence interval is often referred to as the "margin of error." It represents the range within which you expect the true parameter to be with a given level of confidence. A narrower interval indicates greater precision, while a wider interval reflects less precision.

A 90% confidence level is commonly used in statistical analysis when a moderate level of confidence is acceptable. Researchers and analysts often choose the confidence level based on the specific research question, objectives, and the acceptable level of risk. Higher confidence levels, such as 95% or 99%, provide greater confidence but result in wider confidence intervals, which may be less precise. Lower confidence levels, like 80%, provide narrower intervals but come with a slightly higher risk of not containing the true parameter. The choice of confidence level depends on the trade-off between precision and risk that is appropriate for the analysis.