The Function of a Normal Curve: Statistical Distribution

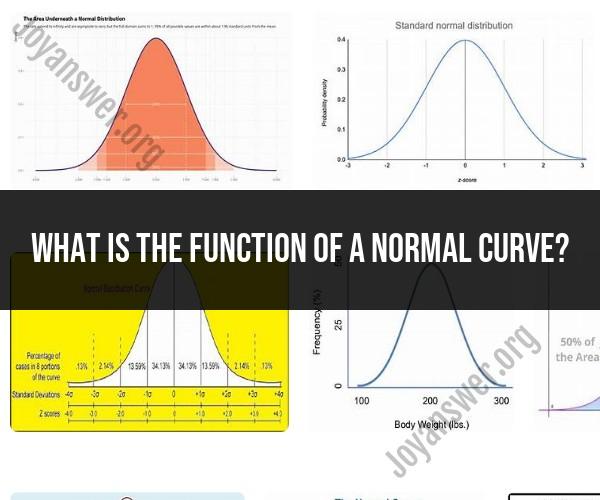
A normal curve, also known as a Gaussian curve or a bell curve, is a symmetrical probability distribution that has several important functions in statistics and probability theory. The primary function of a normal curve is to describe the distribution of data or random variables in a variety of real-world situations. Here are some key functions and properties of a normal curve:

1. Describing Data Distribution: The normal curve is often used to model the distribution of data in situations where the data follows a bell-shaped pattern. Many natural phenomena and human attributes, such as heights, weights, test scores, and IQ scores, tend to be approximately normally distributed.

2. Central Limit Theorem: The normal curve plays a fundamental role in the Central Limit Theorem, which states that the sampling distribution of the sample mean (averages) of a large number of independent and identically distributed random variables will be approximately normally distributed, regardless of the shape of the original population distribution. This theorem is crucial in inferential statistics.

3. Statistical Inference: In hypothesis testing and confidence interval estimation, the normal curve is used as the theoretical basis for making statistical inferences. It helps in determining the likelihood of observing certain sample statistics under different conditions.

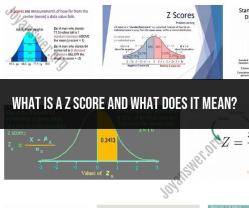
4. Z-Scores: The normal curve is used to calculate z-scores (standard scores), which indicate how many standard deviations a data point is from the mean. Z-scores are essential for comparing and interpreting data across different distributions.

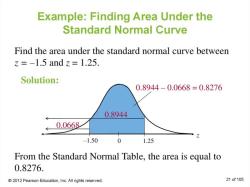
5. Probability Calculations: The area under the normal curve represents probabilities. By calculating the area between specific values on the curve, you can determine the probability of observing data within a certain range. This is often used in statistical hypothesis testing and confidence interval construction.

6. Parameter Estimation: In many statistical estimation techniques, the normal distribution is used as an assumed underlying distribution. Maximum likelihood estimation and least squares regression are examples where the normal distribution is frequently assumed.

7. Quality Control: In quality control and process management, the normal curve is used to monitor and control processes. It helps in identifying deviations from expected performance.

8. Risk Assessment: In finance and risk assessment, the normal distribution is used to model asset returns, price movements, and risk factors in various financial models.

9. Predictive Modeling: In predictive modeling and machine learning, the normal distribution assumption is sometimes used for modeling errors or residuals in regression analysis.

Overall, the normal curve serves as a fundamental tool for statisticians and researchers to understand, model, and analyze data distributions. Its mathematical properties, including symmetry and well-defined probabilities, make it a versatile and widely applicable probability distribution.