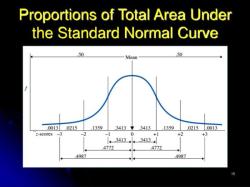
What is the formula for finding the standard deviation?
The standard deviation is a measure of the amount of variation or dispersion in a set of values. The formula for calculating the standard deviation (σ) of a set of data points is as follows:
For a Population:
- is the number of data points in the population.
- represents each individual data point.
- is the mean (average) of the data points.
- denotes the sum across all data points.
- represents the square root.
For a Sample:
- is the number of data points in the sample.
- represents each individual data point.
- is the sample mean (average).
- denotes the sum across all data points.
- represents the square root.
- Note: The denominator is instead of when calculating the standard deviation for a sample. This is known as Bessel's correction and corrects the bias in the estimation of the population standard deviation from a sample.
In words, the formula calculates the square root of the average of the squared differences between each data point and the mean of the data set. The purpose of squaring the differences is to ensure that all values are positive and to give more weight to larger deviations from the mean. The square root is then taken to bring the measurement back to the original units of the data.
Unlocking statistical insights: The formula for finding standard deviation
Standard deviation is a measure of how spread out a set of data is. It is calculated by taking the square root of the variance, which is the average of the squared deviations from the mean.
The formula for finding standard deviation is as follows:
σ = √(∑(x - μ)2 / n)
where:
- σ is the standard deviation
- x is a value in the data set
- μ is the mean of the data set
- n is the number of values in the data set
Step-by-step guide: How to calculate standard deviation by hand
To calculate standard deviation by hand, follow these steps:
- Calculate the mean of the data set.
- Subtract the mean from each value in the data set.
- Square the difference between each value and the mean.
- Add up the squared differences.
- Divide the sum of the squared differences by the number of values in the data set.
- Take the square root of the result.
Excel wizardry: Using spreadsheet functions for standard deviation
Excel has a built-in function for calculating standard deviation, called STDEV.P. To use this function, simply enter the following formula into a cell:
=STDEV.P(data_range)
where data_range is the range of cells that contains the data set.
For example, if the data set is contained in cells A1 to A10, you would enter the following formula into cell B1:
=STDEV.P(A1:A10)
When you press Enter, Excel will display the standard deviation of the data set in cell B1.
Real-world examples: Applying standard deviation in different fields
Standard deviation is used in a variety of fields, including:
- Statistics: Standard deviation is used to calculate confidence intervals and to test hypotheses.
- Finance: Standard deviation is used to measure the risk of an investment.
- Engineering: Standard deviation is used to measure the quality of a manufacturing process.
- Science: Standard deviation is used to measure the accuracy of an experiment.
Mastering standard deviation: Resources for further learning
If you want to learn more about standard deviation, there are a number of resources available online and in libraries. Here are a few suggestions:
- Khan Academy: Khan Academy has a number of videos and tutorials on standard deviation.
- Statistics for Dummies: Statistics for Dummies is a book that provides a basic introduction to statistics, including standard deviation.
- Introductory Statistics with Applications: Introductory Statistics with Applications is a textbook that covers a variety of statistical topics, including standard deviation.