Calculating the Coefficient of Determination: A Statistical Guide

_{October 20, 2023 by JoyAnswer.org, Category : Statistics}

How to calculate the coefficient of determination? Discover the method for calculating the coefficient of determination, a statistical measure used to assess the quality of regression models.

Table of Contents

How to calculate the coefficient of determination?

The coefficient of determination, often denoted as $R^2$ , is a statistical measure that assesses the proportion of the variance in the dependent variable that can be explained by the independent variables in a regression model. It ranges from 0 to 1, with a higher value indicating a better fit of the model to the data. There are different ways to calculate $R^2$ depending on the type of regression (simple or multiple) and the software or tools you're using. Here are the general formulas:

1. For Simple Linear Regression:

In simple linear regression, there's one independent variable and one dependent variable. The formula to calculate $R^2$ is as follows:

$R^2 = \left(\frac{\sum_{i=1}^n (y_i - \hat{y})^2}{\sum_{i=1}^n (y_i - \bar{y})^2}\right)$

Where:

$n$ is the number of data points.
$y_i$ is the observed value of the dependent variable for the $i$ th data point.
$\hat{y}$ is the predicted value of the dependent variable for the $i$ th data point based on the regression model.
$\bar{y}$ is the mean of the observed values of the dependent variable.

2. For Multiple Linear Regression:

In multiple linear regression, there are two or more independent variables and one dependent variable. The formula for $R^2$ is:

$R^2 = 1 - \frac{\text{SSR}}{\text{SST}}$

Where:

$SSR$ is the sum of squared residuals (the differences between the observed and predicted values).
$SST$ is the total sum of squares (a measure of the total variation in the dependent variable).

In practice, when using statistical software or tools like Excel, statistical packages, or programming languages (e.g., Python with libraries like NumPy and SciPy), these calculations are handled automatically, and you don't typically need to compute $R^2$ manually.

To calculate $R^2$ in a specific context, you'd perform the regression analysis and obtain the $R^2$ value as an output. It quantifies the goodness of fit of the regression model to your data, indicating how well the independent variables explain the variation in the dependent variable.

Explaining the Coefficient of Determination in Statistics

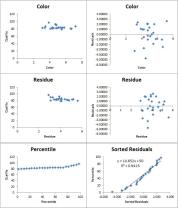
The coefficient of determination, also known as R-squared (R²) or r-squared, is a statistical measure that indicates how well a regression model explains the variation in the dependent variable. It is calculated by dividing the explained sum of squares (ESS) by the total sum of squares (TSS).

Calculating the Coefficient of Determination: Step-by-Step Guide

To calculate the coefficient of determination, follow these steps:

Calculate the explained sum of squares (ESS). The ESS is the sum of the squared deviations of the predicted values from the mean of the dependent variable.
Calculate the total sum of squares (TSS). The TSS is the sum of the squared deviations of the observed values of the dependent variable from the mean of the dependent variable.
Divide the ESS by the TSS. This will give you the coefficient of determination.

Interpreting the Coefficient of Determination in Regression Analysis

The coefficient of determination is a value between 0 and 1. A value of 0 indicates that the regression model does not explain any of the variation in the dependent variable. A value of 1 indicates that the regression model explains all of the variation in the dependent variable.

In general, a higher coefficient of determination indicates a better fit of the regression model to the data. However, it is important to note that the coefficient of determination is not a perfect measure of goodness of fit. It is possible to have a high coefficient of determination even if the regression model is not a good fit for the data.

The Significance of R-squared Values in the Coefficient of Determination

The R-squared value in the coefficient of determination is significant because it indicates the proportion of the variation in the dependent variable that is explained by the independent variable(s). A higher R-squared value indicates that the independent variable(s) are better at explaining the variation in the dependent variable.

Comparing the Coefficient of Determination to Other Statistical Measures

The coefficient of determination can be compared to other statistical measures, such as the adjusted R-squared and the correlation coefficient. The adjusted R-squared is a modification of the coefficient of determination that takes into account the number of independent variables in the regression model. The correlation coefficient is a measure of the linear relationship between two variables.

The coefficient of determination is a useful statistical measure for evaluating the fit of a regression model to the data. However, it is important to use it in conjunction with other statistical measures, such as the adjusted R-squared and the correlation coefficient, to get a more complete picture of the relationship between the independent and dependent variables.

Here are some additional things to keep in mind about the coefficient of determination:

The coefficient of determination is not a measure of causality. Just because a regression model has a high coefficient of determination does not mean that the independent variable(s) cause the dependent variable.
The coefficient of determination can be misleading if the regression model is not well-specified. For example, if the regression model does not include all of the relevant independent variables, the coefficient of determination will be underestimated.
The coefficient of determination can be sensitive to outliers. If the regression model includes outliers, the coefficient of determination may be overestimated.

Overall, the coefficient of determination is a useful statistical measure for evaluating the fit of a regression model to the data. However, it is important to use it in conjunction with other statistical measures and to be aware of its limitations.