Coefficient of Determination (R-squared): Understanding Its Significance
November 6, 2023 by JoyAnswer.org, Category : Statistics
Is are squared the coefficient of determination? Learn what the coefficient of determination (R-squared) represents in statistical analysis and its role in explaining the variance in data.
- 1. Is are squared the coefficient of determination?
- 2. R-squared as the Coefficient of Determination: Clarifying the Connection
- 3. Understanding R-squared as a Coefficient of Determination
- 4. R-squared and the Coefficient of Determination in Statistics
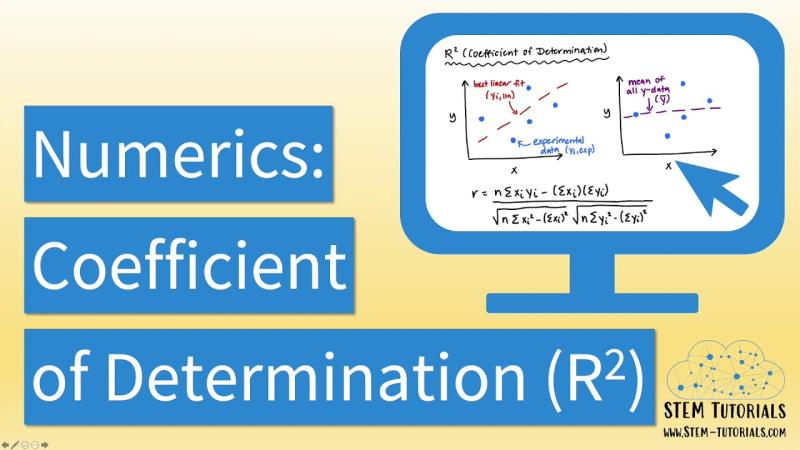
Is are squared the coefficient of determination?
The term "R-squared" is often used to refer to the coefficient of determination, but there's a little confusion in your question. The coefficient of determination is not "are squared." It's actually a statistical measure that represents the proportion of the variance in the dependent variable that is predictable from the independent variables in a regression analysis.
The coefficient of determination, often denoted as R-squared, is a value between 0 and 1, and it indicates the goodness of fit of a regression model. Specifically, it tells you how well the independent variables in the model explain the variability in the dependent variable. Here's what R-squared means:
R-squared = 0: This means that none of the variance in the dependent variable is explained by the independent variables. The model provides no useful information for predicting the dependent variable.
R-squared = 1: In this case, the model perfectly predicts the dependent variable's variance, and all data points fall exactly on the regression line.
R-squared between 0 and 1: This is the typical scenario. The closer R-squared is to 1, the better the model explains the variance in the dependent variable. For example, an R-squared of 0.80 means that the model explains 80% of the variance, and the remaining 20% is unexplained or due to other factors.
In summary, R-squared, the coefficient of determination, is a valuable statistic in regression analysis that helps assess how well the independent variables in a model predict the variability in the dependent variable. It is not "are squared," but rather a numerical measure of the model's goodness of fit.
The term "coefficient of determination" and "R-squared" are often used interchangeably in statistics. While they are closely related concepts, there are some subtle distinctions between the two.
Coefficient of Determination
The coefficient of determination, denoted by R², is a statistical measure that quantifies the proportion of the variance in a dependent variable that is predictable from an independent variable or set of independent variables in a regression model. In other words, it indicates how well the independent variables explain or account for the variation in the dependent variable.
R-squared
R-squared (R²) is the square of the Pearson correlation coefficient (r), which measures the strength and direction of the linear relationship between two variables. It is expressed as a value between 0 and 1, where 0 indicates no correlation and 1 indicates a perfect correlation.
Relationship between R-squared and Coefficient of Determination
R-squared is a specific type of coefficient of determination, specifically applied in the context of linear regression. It provides a measure of how well the linear regression model fits the data. A higher R-squared value indicates a better fit, meaning that the independent variables explain a larger proportion of the variance in the dependent variable.
Understanding R-squared as a Coefficient of Determination
R-squared can be interpreted as the percentage of the total variation in the dependent variable that is explained by the independent variables in the regression model. It is a valuable tool for assessing the goodness of fit of a regression model and comparing the relative performance of different models.
Interpretation of R-squared
0.0-0.25: Weak correlation, indicating that the independent variables explain a small proportion of the variation in the dependent variable.
0.25-0.50: Moderate correlation, indicating that the independent variables explain a fair proportion of the variation in the dependent variable.
0.50-0.75: Strong correlation, indicating that the independent variables explain a significant proportion of the variation in the dependent variable.
0.75-1.00: Very strong correlation, indicating that the independent variables explain a very large proportion of the variation in the dependent variable.
Limitations of R-squared
While R-squared is a useful measure, it is important to note that it is not the only factor to consider when evaluating a regression model. Other factors, such as the statistical significance of the independent variables and the presence of outliers, should also be taken into account.
R-squared and the Coefficient of Determination in Statistics
R-squared and the coefficient of determination are essential concepts in statistical analysis, particularly in the context of regression modeling. They provide valuable insights into the relationships between variables and the effectiveness of statistical models in explaining observed data.
Applications of R-squared and the Coefficient of Determination
Assessing the goodness of fit of regression models
Comparing the relative performance of different regression models
Evaluating the strength of the relationship between variables
Identifying the most important variables in a regression model
Making predictions about the dependent variable based on the independent variables
R-squared and the coefficient of determination are powerful tools for understanding and interpreting data, making them essential for various statistical applications and research endeavors.
