Solving Vertical Curve Problems: Practical Solutions

_{December 5, 2023 by JoyAnswer.org, Category : Engineering}

How to solve vertical curve? Gain insights into solving vertical curve-related challenges. This article offers practical methods and solutions to address problems associated with designing and navigating vertical curves in civil engineering.

How to solve vertical curve?

Solving vertical curve problems involves designing or analyzing the geometry of a road or railway to ensure smooth transitions between different grades (elevations). The primary goal is to create a continuous and safe alignment for vehicles or trains. Here's a step-by-step guide on how to solve vertical curve problems:

For Designing Vertical Curves:

1. Understand Design Criteria:

Know the design speed, desired stopping sight distance, and other relevant design criteria for the road or railway.

2. Determine Initial and Final Grades:

Identify the initial and final grades of the road or railway. These are the grades at the beginning and end of the vertical curve.

3. Calculate the Vertical Curve Length:

Use the stopping sight distance and design speed to calculate the required length of the vertical curve. The formula for length (L) is often based on the design speed and rate of change of grade.

4. Choose the Appropriate Curve Formula:

Select a suitable formula for the vertical curve, such as the Parabolic formula (used in highway design). This formula provides a smooth transition between grades.

5. Calculate Curve Parameters:

Use the chosen curve formula to calculate the curve parameters, such as the algebraic difference in grades and the distance from the beginning of the curve to the point of vertical intersection.

6. Verify Design Standards:

Ensure that the designed vertical curve meets safety and design standards, including visibility requirements and driver expectations.

7. Consider Drainage and Superelevation:

Account for drainage considerations and superelevation (banking of curves) if applicable to the design.

For Analyzing Existing Vertical Curves:

1. Collect Data:

Gather information on the existing road or railway, including grades, elevations, and curve characteristics.

2. Calculate Grades:

Determine the existing grades at the beginning and end of the vertical curve.

3. Verify Sight Distances:

Check stopping sight distances and other visibility requirements to ensure safety.

4. Evaluate Smoothness:

Assess the smoothness of the vertical curve by analyzing the rate of change of grade. Sudden changes may indicate the need for adjustments.

5. Identify Issues:

Look for potential issues such as limited sight distance, excessive grades, or inadequate transition lengths.

6. Propose Adjustments:

If issues are identified, propose adjustments to the vertical curve, such as modifying grades or extending the curve length.

7. Consider Safety Improvements:

Consider safety improvements, such as adding transition tapers, adjusting superelevation, or enhancing visibility.

8. Ensure Compliance:

Verify that the existing vertical curve complies with current design standards and regulations.

Solving vertical curve problems requires a combination of engineering judgment, adherence to design standards, and a thorough understanding of the specific conditions of the road or railway. Always consider safety, visibility, and smooth transitions when designing or analyzing vertical curves.

What methods or procedures are involved in solving vertical curve problems?

Solving vertical curve problems involves determining the appropriate curve type, calculating the curve elements, and establishing the elevation profile of the curve. The specific methods and procedures vary depending on the type of vertical curve and the desired level of precision.

Types of Vertical Curves

There are two main types of vertical curves:

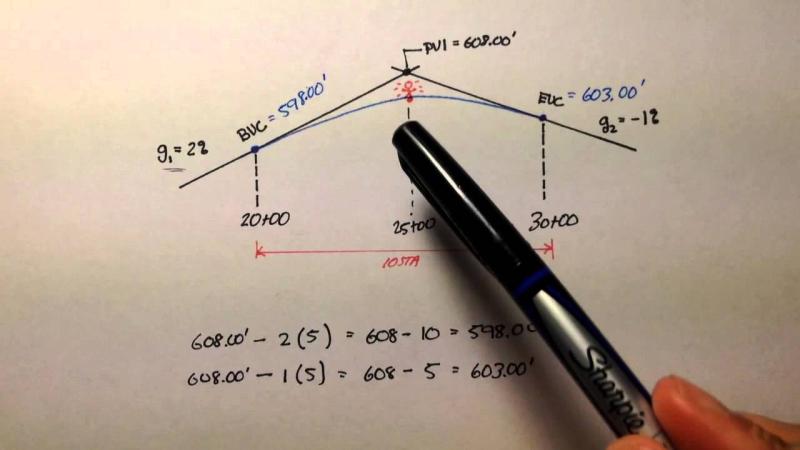
Parabolic curves: Parabolic curves are the most common type of vertical curve due to their smooth and consistent curvature. They are defined by the equation:

y = Ax^2 + Bx + C

where:

y is the elevation of the curve at a distance x from the PVC

A, B, and C are constants that define the shape of the curve

Circular curves: Circular curves are less common than parabolic curves but can be used in situations where a steeper change in grade is required. They are defined by the equation:

y = R^2 - (R - x)^2)^(1/2) + HPI

where:

y is the elevation of the curve at a distance x from the PVI

R is the radius of the curve

HPI is the elevation of the PVI

Calculating Curve Elements

The curve elements are the parameters that define the shape and size of the vertical curve. These elements include:

PVC (Point of Vertical Curvature): The PVC is the point where the vertical curve begins to transition from one grade to another.

PVI (Point of Vertical Intersection): The PVI is the point where the two tangent grades intersect.

Grade: The grade is the slope of the roadway expressed as a percentage.

Length (L): The length is the total distance along the curve.

Vertical difference (ΔE): The vertical difference is the change in elevation between the PVC and the PVI.

A-value: The A-value is a constant that defines the shape of the parabola.

R-value: The R-value is the radius of the circular curve.

Establishing Elevation Profile

The elevation profile is a graphical representation of the vertical curve, showing the elevation of the roadway at any point along the curve. The elevation profile can be calculated using the formula for the curve type or by using a computer program.

Methods for Solving Vertical Curve Problems

There are several methods for solving vertical curve problems, including:

Algebraic method: This method involves solving a system of equations to determine the curve elements.

Graphical method: This method involves drawing the curve to scale and then measuring the curve elements.

Computer-aided design (CAD) software: This method involves using CAD software to create a model of the curve and then calculating the curve elements.

Factors Influencing Vertical Curve Design

Several factors influence the design of vertical curves, including: