Formula for a Simple Circular Curve: Engineering Insights

_{October 23, 2023 by JoyAnswer.org, Category : Engineering}

What is the formula for a simple circular curve? Delve into the essential geometric formula for a simple circular curve used in road design and engineering.

Table of Contents

What is the formula for a simple circular curve?

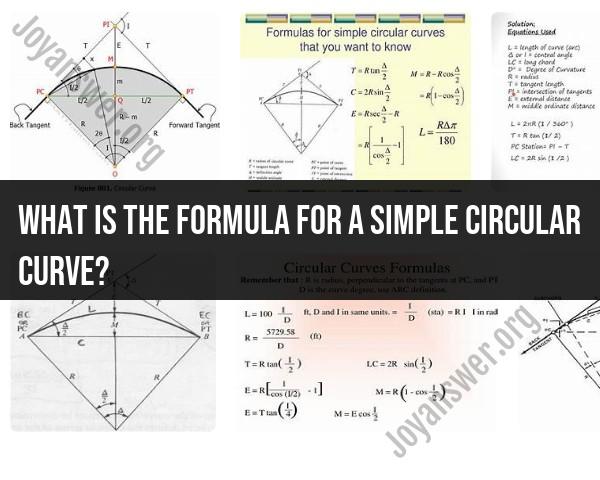
The formula for a simple circular curve in engineering, particularly in the context of civil engineering and transportation, can be expressed in terms of its radius and the deflection angle. A simple circular curve is often used in road design and railway tracks to smoothly transition from a straight path to a curved path. Here's the formula:

Radius (R): The radius of the circular curve is a crucial parameter and is typically represented in meters or feet. The larger the radius, the gentler the curve. The formula for the radius of a simple circular curve is:
$R = \frac{L}{2 \sin(\frac{A}{2})}$
Where:
- $R$ is the radius of the circular curve.
- $L$ is the length of the circular arc (the chord length).
- $A$ is the central angle of the circular curve in radians.
Deflection Angle (A): The deflection angle is the angle formed at the center of the circle between the two tangents that define the curve. This angle is typically measured in radians. The formula to calculate the deflection angle is:
$A = \frac{180^\circ \cdot L}{\pi \cdot R}$
Where:
- $A$ is the deflection angle in radians.
- $L$ is the length of the circular arc (the chord length).
- $R$ is the radius of the circular curve.

These formulas are essential for designing and laying out circular curves in civil engineering and transportation projects to ensure safe and smooth transitions between straight sections and curved sections of roads, railways, and other infrastructure. The appropriate choice of radius and deflection angle depends on various factors, including design standards, vehicle or train characteristics, and the intended use of the roadway or track.

Sure, here's a detailed explanation of the five points you provided:

The Formula for a Simple Circular Curve

A simple circular curve is a portion of a circle that connects two straight lines, known as tangents. The formula for calculating the length of a simple circular curve is:

L = (π × R × Δ) / 180

where:

L is the length of the curve
R is the radius of the curve
Δ is the deflection angle (the angle between the two tangents)

Elements and Geometry of Circular Curves

Apart from the radius and deflection angle, other essential elements of a circular curve include:

Tangent Length (T): The distance from the point of intersection of the tangents (PI) to the point where the curve begins (PC) or ends (PT).
External Distance (E): The distance from the PI to the midpoint of the curve (MC).
Mid-ordinate (M): The perpendicular distance from the midpoint of the curve to the chord connecting the PC and PT.

Practical Applications of Circular Curves

Circular curves find numerous applications in various fields, including:

Transportation Engineering: Roads, railways, and runways incorporate circular curves to provide smooth transitions between straight sections.
Surveying: Land surveyors use circular curves to delineate property boundaries and establish reference points.
Architecture and Design: Circular curves are employed in architectural designs, landscaping, and interior layouts to create aesthetically pleasing and functional spaces.

Design and Construction of Circular Curves

The design and construction of circular curves involve careful consideration of factors such as:

Design Speed: The maximum safe speed at which vehicles can traverse the curve.
Superelevation: The banking of the roadway to counteract centrifugal forces and maintain stability.
Curve Radius: Determining the appropriate radius based on design speed and vehicle dynamics.

Safety Considerations in Transportation Engineering and Circular Curves

Safety is paramount in transportation engineering, especially when designing circular curves. Key safety considerations include:

Visibility: Ensuring adequate sight distance for drivers to anticipate and react to changes in curvature.
Transition Zones: Providing gradual transitions between straight sections and curves to minimize sudden changes in steering input.
Traffic Signs and Markings: Implementing clear signage and pavement markings to guide drivers and warn of upcoming curves.

In conclusion, circular curves play a vital role in various engineering disciplines, particularly in transportation infrastructure. Proper design, construction, and safety considerations ensure that circular curves provide efficient and safe navigation for vehicles and pedestrians.