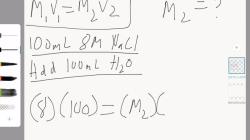Equilibrium Equation: Understanding the Formula

_{November 6, 2023 by JoyAnswer.org, Category : Science}

What is the equation for this equilibrium? Learn about the equilibrium equation and its application in various scientific fields, particularly in the context of chemical equilibrium.

Table of Contents

What is the equation for this equilibrium?

Equilibrium in a chemical reaction is a state where the rates of the forward and reverse reactions are equal, and the concentrations of the reactants and products remain constant over time. The equation that describes the equilibrium for a chemical reaction is called the equilibrium expression or equilibrium constant expression. It's usually written in the following general form:

aA + bB ⇌ cC + dD

In this equation:

"a" and "b" are the coefficients of the reactants A and B.
"c" and "d" are the coefficients of the products C and D.

The double arrow (⇌) indicates that the reaction is in a state of dynamic equilibrium, where the forward reaction (from left to right) and the reverse reaction (from right to left) are occurring at the same rate.

The equilibrium constant (K) for this reaction is expressed as:

K = [C]^c [D]^d / [A]^a [B]^b

In this expression:

[C] and [D] are the molar concentrations of the products C and D at equilibrium.
[A] and [B] are the molar concentrations of the reactants A and B at equilibrium.

The values of a, b, c, and d in the equilibrium expression are determined by the balanced chemical equation for the reaction. The equilibrium constant (K) is a numerical value that characterizes the position of the equilibrium and helps predict the direction in which the reaction will proceed under certain conditions. If K is much greater than 1, the equilibrium lies to the right, indicating that the products are favored. If K is much less than 1, the equilibrium lies to the left, indicating that the reactants are favored. If K is close to 1, the concentrations of reactants and products are roughly equal at equilibrium.

Equilibrium Equations: Formulas for Finding Balance

Equilibrium equations are mathematical expressions that describe the relationships between forces and moments acting on a system in a state of equilibrium. These equations are fundamental principles in various fields, including physics, engineering, and chemistry. They provide a powerful tool for analyzing and predicting the behavior of systems under various conditions.

The general form of an equilibrium equation is:

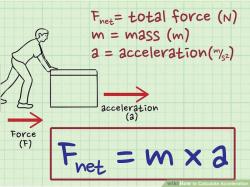
∑F = 0

where ∑F represents the vector sum of all forces acting on a system. This equation states that for a system to be in equilibrium, the net force acting on it must be zero.

In addition to the force equilibrium equation, there is also a moment equilibrium equation:

∑M = 0

where ∑M represents the vector sum of all moments acting on a system. This equation states that for a system to be in equilibrium, the net moment acting on it must also be zero.

The specific forms of the equilibrium equations will vary depending on the type of system being analyzed. For example, for a system of particles, the equilibrium equations can be expressed in terms of the forces acting on each individual particle. For a rigid body, the equilibrium equations can be expressed in terms of the forces and moments acting on the center of mass of the body.

Exploring the Equilibrium Equation in Various Contexts

Equilibrium equations have a wide range of applications in various fields. Here are a few examples:

Physics: Equilibrium equations are used to analyze the motion of objects, such as the motion of a ball thrown into the air or the motion of a car traveling down a road.
Engineering: Equilibrium equations are used to design structures, such as bridges and buildings, to ensure that they can withstand the forces acting on them.
Chemistry: Equilibrium equations are used to describe chemical reactions and to predict the equilibrium concentrations of reactants and products.

Understanding and Using Equilibrium Formulas

To use equilibrium equations effectively, it is important to understand the following concepts:

Free-body diagrams: Free-body diagrams are graphical representations of all the forces acting on a system. They are essential for identifying and analyzing the forces acting on a system.
Sign conventions: Sign conventions are used to determine the positive and negative directions of forces and moments. It is important to use consistent sign conventions to avoid errors in calculations.
Vector algebra: Vector algebra is used to manipulate vectors, such as forces and moments. This includes adding, subtracting, and multiplying vectors.

With a good understanding of these concepts, you can apply equilibrium equations to solve a variety of problems involving forces and moments.