How to calculate a phasor from a time domain quantity?
Calculating phasors from time-domain quantities is a fundamental concept in electrical analysis, especially in the field of AC (alternating current) circuit analysis. Phasors are complex numbers that represent sinusoidal voltage or current waveforms in a simplified, time-independent form. They are used to simplify complex AC calculations and facilitate the analysis of electrical circuits. In this guide, we'll provide a comprehensive and detailed explanation of how to calculate phasors from time-domain quantities.
1. Understanding Time-Domain Quantities:
- Time-domain quantities are those that vary with time, such as voltage (V(t)) or current (I(t)) in an AC circuit.
- These quantities are typically described by trigonometric functions, such as sine or cosine waves.
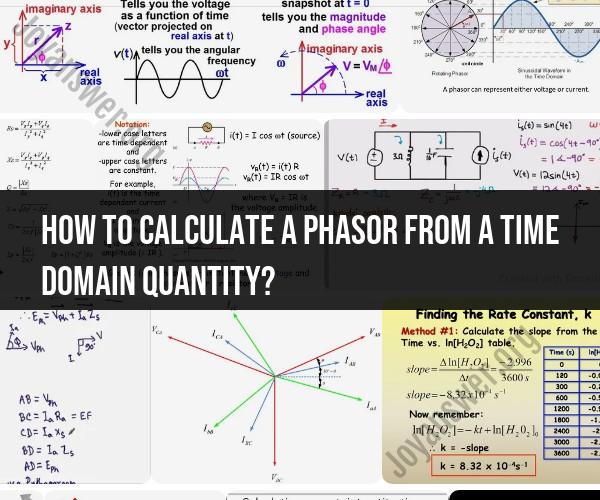
2. Phasor Representation:
- A phasor is a complex number that represents the amplitude and phase of a sinusoidal waveform.
- Phasors are typically expressed in the form: A∠θ, where A is the magnitude (amplitude) of the waveform, and θ is the phase angle.
3. Calculating Phasors:
- To calculate a phasor from a time-domain quantity, follow these steps:
a. Express the time-domain quantity in its trigonometric form. For example, a sinusoidal voltage can be represented as V(t) = Vm * cos(ωt + φ), where Vm is the peak amplitude, ω is the angular frequency, t is time, and φ is the phase angle.
b. Identify the peak amplitude (Vm) and the phase angle (φ) from the trigonometric expression.
c. Write the phasor in polar form: A∠θ, where A is the magnitude and θ is the phase angle. In this case, A = Vm and θ = φ.
d. The phasor can also be represented in rectangular (or Cartesian) form as A(cos θ + j*sin θ), where j represents the imaginary unit.
- It's important to note that for voltage phasors, the reference direction (usually assumed to be a horizontal axis) is typically the starting point for measuring the phase angle.
4. Example:Let's consider an example:V(t) = 10 * cos(1000t - π/4) VIn this case:
- Vm = 10 V (peak amplitude)
- φ = -π/4 radians (phase angle)
The phasor representation is: V∠θ = 10∠(-π/4).
5. Applications:
- Phasors are commonly used in AC circuit analysis to simplify calculations involving complex AC voltages and currents.
- They facilitate the use of algebraic methods (instead of calculus) to solve AC circuit problems.
- Phasor diagrams are often used to visualize the relationships between different AC quantities in a circuit.
In conclusion, calculating phasors from time-domain quantities involves expressing the time-domain quantity in trigonometric form and then extracting the amplitude and phase angle. Phasors are essential tools in AC circuit analysis and help simplify complex calculations, making them a valuable concept in electrical engineering.