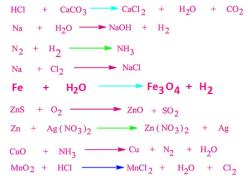
Can we add the voltages in the time domain?
Yes, voltages can be added in the time domain. When you add voltages in the time domain, you are essentially combining different voltage waveforms that vary over time. This is a fundamental concept in electrical engineering and electronics, and it is often used when analyzing and designing electrical circuits.
In the time domain, voltage waveforms are represented as functions of time. When you add two or more voltage waveforms together, you simply sum the instantaneous voltages at each point in time. Mathematically, this can be expressed as:
V(t) = V1(t) + V2(t) + V3(t) + ...
Where:
- V(t) is the resulting voltage waveform at time t.
- V1(t), V2(t), V3(t), etc., are the individual voltage waveforms that you want to add together.
The addition of voltages in the time domain is based on the principle of superposition, which states that the response of a linear system to the sum of multiple inputs is equal to the sum of the responses of the system to each individual input.
This concept is widely used in electrical circuit analysis, signal processing, and many other areas of electronics. For example, when analyzing the behavior of a circuit with multiple voltage sources, you can add the voltages from each source to determine the total voltage across a particular component or node in the circuit.
It's important to note that this principle is applicable to linear systems. In nonlinear systems, the addition of voltages in the time domain may not hold true, and more complex mathematical techniques may be required to analyze the behavior of the system.
Example:Let's consider two voltage waveforms, V1(t) and V2(t), and we want to find the resulting voltage waveform V(t) when they are added together.
- V1(t) represents a sinusoidal voltage waveform: V1(t) = 5 sin(2πf1t), where f1 is the frequency.
- V2(t) represents a square wave voltage: V2(t) = 3 for 0 ≤ t ≤ T/2 and V2(t) = -3 for T/2 ≤ t ≤ T, where T is the period.
We want to find the resulting voltage waveform V(t) when V1(t) and V2(t) are added together.
Solution:To find V(t), we simply add V1(t) and V2(t) at each point in time:
For 0 ≤ t ≤ T/2:V(t) = V1(t) + V2(t) = 5 sin(2πf1t) + 3
For T/2 ≤ t ≤ T:V(t) = V1(t) + V2(t) = 5 sin(2πf1t) - 3
In this example, we've added a sinusoidal voltage waveform and a square wave voltage waveform in the time domain to obtain the resulting voltage waveform V(t). The resulting waveform will be a combination of these two waveforms with their respective amplitudes and frequencies.