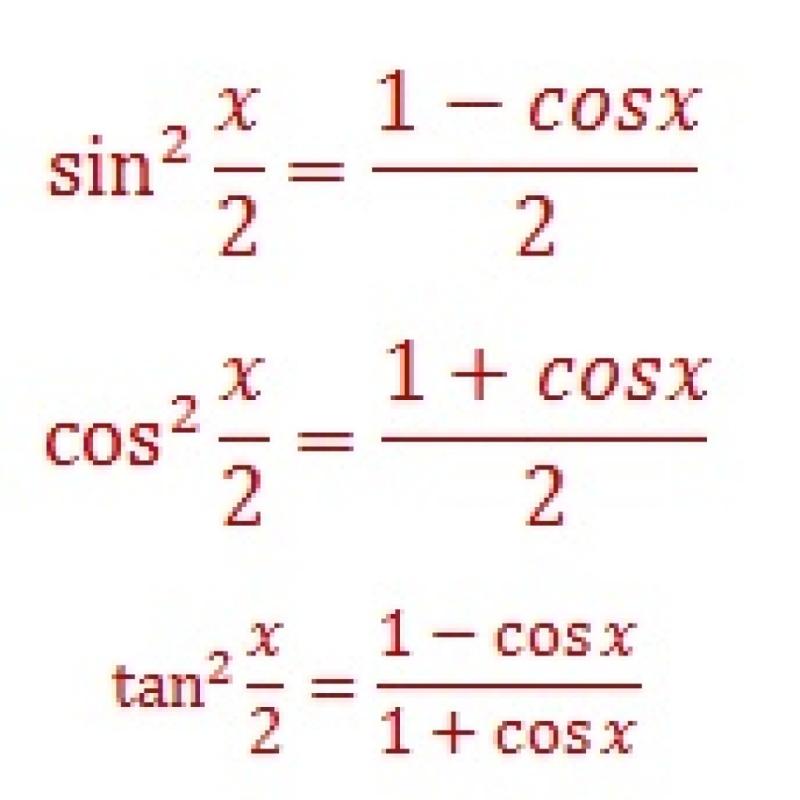Understanding Half-Angle Identities in Trigonometry

_{November 23, 2023 by JoyAnswer.org, Category : Mathematics}

What are half angle identities? Learn about half-angle identities in trigonometry. Explore the formulas and equations related to expressing trigonometric functions of half-angles.

Table of Contents

What are half angle identities?

In trigonometry, half-angle identities express the trigonometric functions of half of an angle in terms of the original angle. These identities are derived from the double-angle identities and are useful in simplifying expressions and solving problems in trigonometry. The half-angle identities are typically expressed in terms of sine, cosine, and tangent functions. Here are the half-angle identities:

Sine Half-Angle Identity: $\sin\left(\frac{\theta}{2}\right) = \pm \sqrt{\frac{1 - \cos(\theta)}{2}}$
The choice of the positive or negative square root depends on the quadrant in which the original angle $\theta$ lies.
Cosine Half-Angle Identity: $\cos\left(\frac{\theta}{2}\right) = \pm \sqrt{\frac{1 + \cos(\theta)}{2}}$
As with the sine half-angle identity, the choice of the positive or negative square root depends on the quadrant of the original angle.
Tangent Half-Angle Identity: $\tan\left(\frac{\theta}{2}\right) = \pm \sqrt{\frac{1 - \cos(\theta)}{1 + \cos(\theta)}}$
Again, the choice of the positive or negative square root depends on the quadrant of the original angle.

These half-angle identities are especially useful when dealing with trigonometric expressions involving angles that are halved. They provide a way to express trigonometric functions at half angles in terms of the original angles, facilitating the simplification of expressions and calculations. The choice of the positive or negative square root is determined by the quadrant of the original angle, and it is important to consider this when applying the identities in problem-solving.

Sure, here are the answers to your questions about half-angle identities in trigonometry:

What are half-angle identities in trigonometry?

Half-angle identities in trigonometry are mathematical equations that relate the trigonometric functions of a half-angle to the trigonometric functions of the full angle. These identities are useful for simplifying trigonometric expressions and solving trigonometric equations.

The three main half-angle identities are:

Half-angle identity for sine: sin(A/2) = ±√[(1 - cos A)/2]

Half-angle identity for cosine: cos(A/2) = ±√[(1 + cos A)/2]

Half-angle identity for tangent: tan(A/2) = ±√[(1 - cos A)/(1 + cos A)]

In these formulas, A represents the full angle, and A/2 represents the half-angle. The ± symbol indicates that the sign of the result depends on the quadrant in which the half-angle lies.

How are half-angle identities used in trigonometric equations?

Half-angle identities can be used to simplify trigonometric expressions and solve trigonometric equations in various ways. Here are some examples:

Simplifying trigonometric expressions: Half-angle identities can be used to simplify trigonometric expressions by converting products of trigonometric functions into sums or differences of trigonometric functions.

Solving trigonometric equations: Half-angle identities can be used to solve trigonometric equations by converting equations involving trigonometric functions of a half-angle into equations involving trigonometric functions of the full angle.

Proving trigonometric identities: Half-angle identities can be used to prove other trigonometric identities by substituting them into the original identity and simplifying the resulting expression.

3. Examples of half-angle identities

Here are some examples of how half-angle identities can be used:

Simplifying the expression sin(30°)sin(60°): Using the half-angle identity for sine, we can write:

sin(30°)sin(60°) = sin(30°/2)sin(2*30°/2)= sin(15°)sin(30°)= (1/2)(√3/2)= √3/4

Solving the equation cos(x) = 2sin(x/2): Using the half-angle identity for cosine, we can write:

cos(x) = 2sin(x/2)= 2√[(1 - cos x)/2]= √(1 - cos x)

Squaring both sides, we get:

cos^2(x) = 1 - cos x

Solving for cos x, we find:

cos x = 1/2

Proving the identity sin(2A) = 2sin(A)cos(A): Using the half-angle identity for sine and cosine, we can write:

sin(2A) = 2sin(A)cos(A)= 2sin(A/2)cos(A/2)= 2(√[(1 - cos A)/2])(√[(1 + cos A)/2])= (1 - cos A)(1 + cos A)= 1 - cos^2 A= sin^2 A + cos^2 A= 1 (since sin^2 A + cos^2 A = 1)

Thus, we have proven the identity sin(2A) = 2sin(A)cos(A).