Understanding the Basics of Trigonometry: A Beginner's Guide

_{February 23, 2024 by JoyAnswer.org, Category : Mathematics}

What is basic trigonometry? Get acquainted with the fundamental concepts of trigonometry with this beginner's guide. Explore trigonometric functions, identities, and applications in various fields of mathematics and science.

What is basic trigonometry?

Basic trigonometry is a branch of mathematics that deals with the study of relationships between angles and sides of triangles. It primarily focuses on the trigonometric functions, which are ratios of the lengths of sides in right triangles.

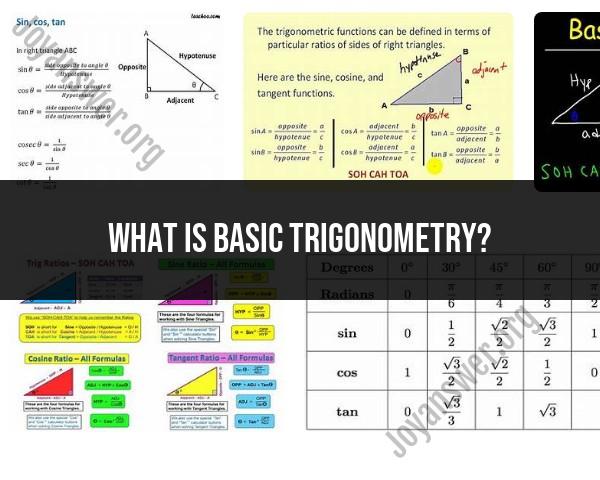
The three primary trigonometric functions are:

Sine (sin): The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. $\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}$
Cosine (cos): The cosine of an angle in a right triangle is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. $\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}$
Tangent (tan): The tangent of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. $\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}$

These functions are fundamental to trigonometry and are used to solve various problems involving triangles, such as finding unknown side lengths or angles.

In addition to these basic trigonometric functions, trigonometry also involves concepts such as angles (measured in degrees or radians), the Pythagorean theorem, trigonometric identities, and the unit circle.

Trigonometry has numerous applications across various fields, including mathematics, physics, engineering, architecture, astronomy, and more. It provides a powerful tool for analyzing and solving problems related to angles and distances in both theoretical and practical contexts.

Trigonometry: Unveiling the Secrets of Triangles

Trigonometry, a branch of mathematics, focuses on the relationships between angles and sides of triangles. Here's an exploration of its fundamental concepts, applications, and problem-solving techniques:

1. Fundamental Concepts:

Right Triangles: The foundation of trigonometry lies in right triangles, where one angle is 90 degrees.

Trigonometric Ratios: These ratios relate the lengths of the sides of a right triangle to its angles. The three primary ratios are:
- Sine (sin): Opposite side divided by the Hypotenuse.
- Cosine (cos): Adjacent side divided by the Hypotenuse.
- Tangent (tan): Opposite side divided by the Adjacent side.

Unit Circle: This circle with a radius of 1 unit visually represents the trigonometric ratios for all angles, not just right triangles.

2. Applying Trigonometry to Solve Geometric Problems:

Once you understand the trigonometric ratios, you can solve various geometric problems involving triangles, including:

Finding missing side lengths: Use the appropriate trigonometric ratio based on the given information (angles and other sides) and solve for the unknown side.

Finding missing angles: Utilize inverse trigonometric functions (sin^-1, cos^-1, tan^-1) to determine the angle measure based on a known ratio and side length.

Solving real-world problems: Apply trigonometric concepts to calculate distances, heights, or angles in various scenarios, like finding the height of a building, the distance across a river, or the angle of a launched projectile.

3. Real-World Applications of Basic Trigonometry:

Trigonometry principles have diverse applications beyond traditional geometry, including:

Navigation: Used in determining positions at sea, calculating flight paths, and even navigating satellites.

Engineering: Crucial for designing and analyzing structures like bridges, buildings, and trusses, where understanding load distribution and forces is essential.

Surveying and Mapping: Used in measuring distances and angles to create accurate maps and determine land boundaries.

Computer Graphics: Plays a vital role in 3D animation, video games, and other visual effects, where calculations involving angles and positions are used to create realistic visuals.

Physics: Fundamental for understanding wave behavior (sound, light), analyzing projectile motion, and solving problems involving forces and motion.

By mastering these fundamental concepts and applying them creatively, trigonometry becomes a powerful tool for solving real-world problems across various disciplines.