Magnitude of Normal Force: Understanding its Significance
November 6, 2023 by JoyAnswer.org, Category : Physics
What is the magnitude of a normal force? Gain an understanding of the magnitude of the normal force in physics and its importance in various scenarios involving contact and support.
- 1. What is the magnitude of a normal force?
- 2. Magnitude of a Normal Force: Definition and Calculation
- 3. Understanding Normal Force in Physics and its Magnitude
- 4. Calculating the Strength of Normal Force in Different Scenarios
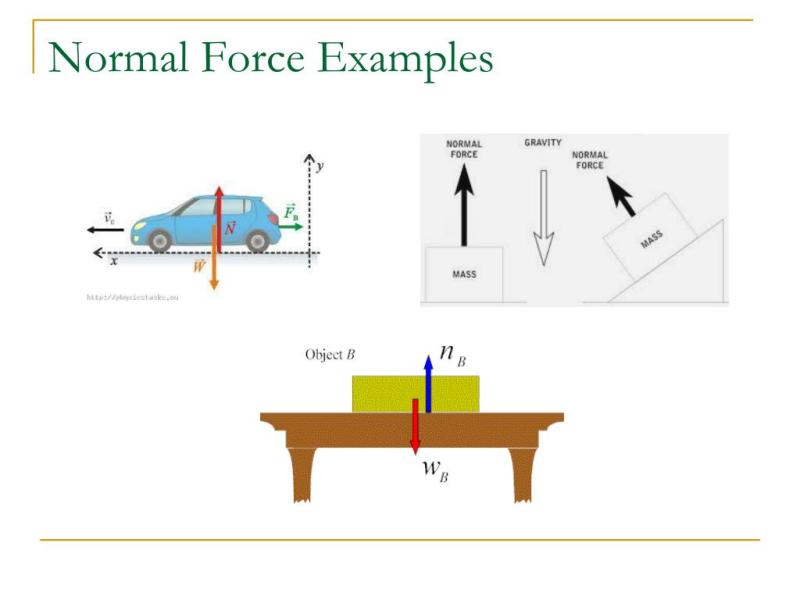
What is the magnitude of a normal force?
The magnitude of a normal force is equal to the force of gravity acting on an object that is in contact with a surface and at rest (or in equilibrium) with respect to that surface. In other words, the normal force represents the force exerted by a surface to support the weight of an object resting on it. The magnitude of the normal force is equal to the weight of the object and is typically calculated using the formula:
Normal Force (N) = Weight (W) = m * g
Where:
- Normal Force (N) is the force exerted by the surface on the object.
- Weight (W) is the gravitational force acting on the object, typically measured in newtons (N).
- m is the mass of the object, typically measured in kilograms (kg).
- g is the acceleration due to gravity, approximately 9.81 m/s² on the surface of the Earth.
The normal force acts perpendicular to the contact surface and counterbalances the force of gravity, preventing the object from falling through the surface. When an object is on a level surface and at rest, the normal force is equal in magnitude and opposite in direction to the force of gravity, which results in a net force of zero, indicating equilibrium.
It's important to note that the magnitude of the normal force can vary if an object is on an inclined surface or subjected to external forces. In such cases, the normal force is adjusted to maintain equilibrium, but its magnitude is still equal to the force required to support the weight of the object.
Understanding the magnitude of the normal force is crucial in physics and engineering for analyzing the equilibrium of objects and structures in contact with surfaces and for calculating the forces involved in various mechanical systems.
Magnitude of a Normal Force: Definition and Calculation
In physics, the normal force (Fn) is the force exerted by a surface on an object perpendicular to the surface when the two are in contact. It is a contact force, meaning it arises from the direct interaction of two surfaces. The magnitude of the normal force is the strength or intensity of this force.
Definition: The magnitude of the normal force (|Fn|) is the absolute value of the normal force. It represents the amount of force pushing perpendicular to the surface.
Calculation: The magnitude of the normal force can be calculated using Newton's second law (F=ma), which states that the net force acting on an object equals its mass multiplied by its acceleration.
For an object resting on a horizontal surface with no external forces acting on it, the normal force is equal to the weight of the object (Fn = W = mg), where m is the object's mass and g is the acceleration due to gravity.
For an object resting on an inclined surface with no external forces acting on it, the magnitude of the normal force is given by Fn = mgcosθ, where θ is the angle of inclination of the surface.
Understanding Normal Force in Physics and its Magnitude
The normal force plays a crucial role in various physical phenomena, such as:
Preventing objects from passing through solid surfaces: The normal force ensures that objects cannot penetrate each other, maintaining the integrity of solid surfaces.
Enabling motion along surfaces: The normal force can influence the motion of an object along a surface by providing a component of force parallel to the surface.
Contributing to friction: The normal force is a factor in determining the frictional force between two surfaces.
The magnitude of the normal force is essential in quantifying the strength of the interaction between two surfaces and its impact on the motion of objects.
Calculating the Strength of Normal Force in Different Scenarios
Consider the following scenarios to illustrate the calculation of the normal force:
Scenario 1: Object on a Horizontal Surface
An object with a mass of 5 kg is resting on a horizontal table. Calculate the magnitude of the normal force acting on the object.
Given: m = 5 kg, g = 9.81 m/s²
Fn = W = mg = 5 kg * 9.81 m/s² = 49.05 N
Scenario 2: Object on an Inclined Plane
An object with a mass of 10 kg is resting on an inclined plane with an angle of inclination of 30 degrees. Calculate the magnitude of the normal force acting on the object.
Given: m = 10 kg, g = 9.81 m/s², θ = 30°
Fn = mgcosθ = 10 kg * 9.81 m/s² * cos(30°) = 86.6 N
Conclusion
The magnitude of the normal force is a fundamental concept in physics, quantifying the strength of the perpendicular force exerted by a surface on an object in contact. Understanding and calculating the normal force is essential in analyzing various physical phenomena and predicting the motion of objects.
