Equations for Calculating Velocity Change

_{January 26, 2024 by JoyAnswer.org, Category : Physics}

What is the equation to find change in velocity? Uncover the equation to calculate changes in velocity. This comprehensive guide provides the necessary formulas and step-by-step instructions for determining the change in velocity in various scenarios.

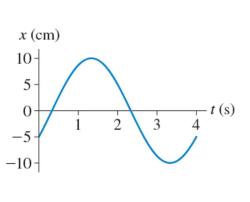
What is the equation to find change in velocity?

The change in velocity, often denoted as $\Delta v$ (delta v), is calculated using the following equation:

$\Delta v = v_f - v_i$

Here:

$\Delta v$ is the change in velocity.
$v_f$ is the final velocity.
$v_i$ is the initial velocity.

This equation simply subtracts the initial velocity from the final velocity to determine the change in velocity. If the final velocity is greater than the initial velocity, the change is positive (indicating an increase in speed), and if the final velocity is less than the initial velocity, the change is negative (indicating a decrease in speed).

It's important to note that velocity is a vector quantity, meaning it has both magnitude and direction. Therefore, when dealing with vector quantities, you need to consider the direction of motion as well. If only magnitudes are considered, the equation becomes:

$\Delta v = |v_f| - |v_i|$

This gives the magnitude of the change in velocity without considering the direction. If direction is important, vector notations should be used in the calculation.

It's also worth mentioning that if the motion is taking place under constant acceleration, the change in velocity can be related to the acceleration ( $a$ ) and time ( $t$ ) using the equation:

$\Delta v = a \cdot t$

Here:

$\Delta v$ is the change in velocity.
$a$ is the acceleration.
$t$ is the time over which the acceleration occurs.

This equation is derived from the definition of acceleration ( $a = \frac{\Delta v}{\Delta t}$ ) by rearranging terms to solve for $\Delta v$ .

Calculating and Representing Change in Velocity: Demystifying the Math

1. Equation for Change in Velocity:

The mathematical equation to calculate the change in velocity (denoted by Δv) is quite simple:

Δv = v_final - v_initial

where:

Δv is the change in velocity

v_final is the final velocity

v_initial is the initial velocity

This equation essentially subtracts the initial velocity from the final velocity to determine how much the velocity has changed (increased or decreased).

2. Representation in Physics and Formulas:

In physics, change in velocity is typically represented as a vector quantity. This means it has both magnitude (how much the velocity has changed) and direction (whether it sped up, slowed down, or changed direction). It is often used in various kinematic equations related to motion, such as:

v_final = v_initial + a * t: This equation calculates the final velocity based on the initial velocity, acceleration (a), and time (t).

Δx = v_average * t: This equation calculates the displacement (Δx) based on the average velocity and time.

a = Δv / t: This equation defines acceleration as the change in velocity over time.

Therefore, understanding change in velocity is crucial for solving different motion problems and analyzing various types of movement.

3. Units and Variables:

The change in velocity, Δv, is measured in the same units as velocity, which is meters per second (m/s). This makes sense as it represents the difference between two velocity values.

The other variables involved in the formulas mentioned above also have specific units: