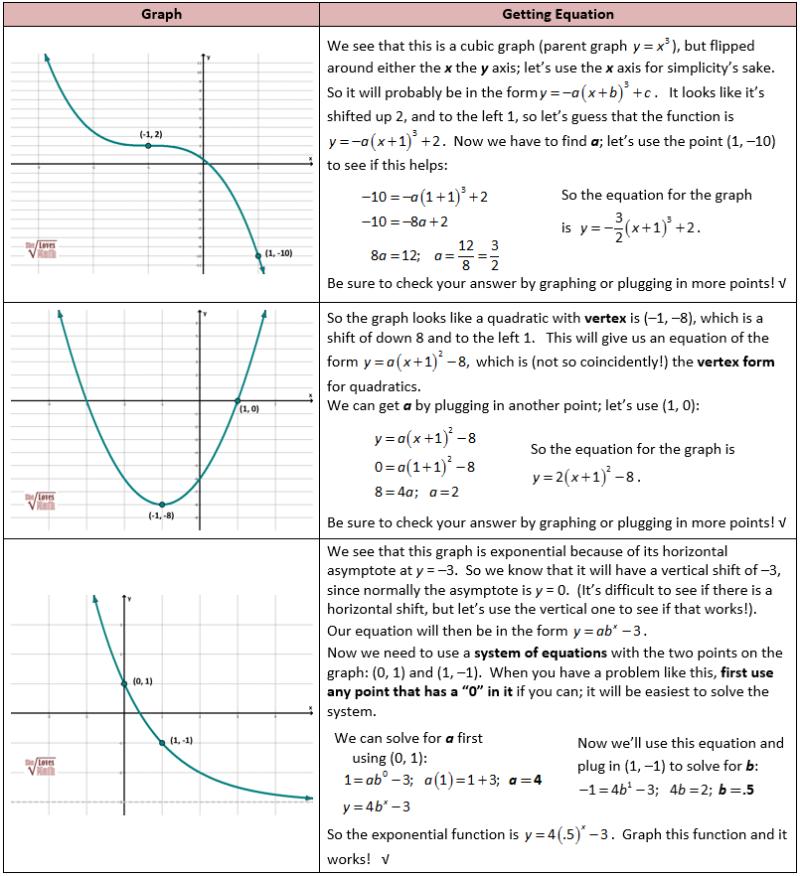
Equational Exploration: How to Find a Parent Function from an Equation

_{November 20, 2023 by JoyAnswer.org, Category : Mathematics}

How to find parent function from equation? Discover the process of identifying a parent function from an equation. This guide provides step-by-step instructions for extracting parent functions from mathematical expressions.

Table of Contents

How to find parent function from equation?

Finding the parent function from an equation involves identifying the basic function that serves as a starting point for transformations. The parent function is typically a simple, standard function that undergoes transformations to create more complex functions. Here are general steps to find the parent function from an equation:

Identify the Key Elements:
- Look for key elements in the equation, such as constants, coefficients, and exponents. These elements provide information about the specific features and transformations applied to the parent function.
Isolate the Transformations:
- Separate the transformations applied to the parent function from the rest of the equation. This involves recognizing changes in the form of the equation that indicate shifts, stretches, compressions, or reflections.
Understand Common Parent Functions:
- Familiarize yourself with common parent functions and their general forms. Some examples of parent functions include linear functions (y = x), quadratic functions (y = x^2), cubic functions (y = x^3), absolute value functions (y = |x|), square root functions (y = √x), and reciprocal functions (y = 1/x).
Identify the Specific Function:
- Determine which parent function corresponds to the transformations indicated in the equation. For example, if the equation involves squaring (x^2), it may be related to a quadratic parent function.
Check for Additional Transformations:
- Some equations may include multiple transformations. Check for additional elements in the equation that indicate shifts along the x-axis or y-axis, changes in amplitude, or reflections.
Verify with Graphs:
- Plot the graph of the equation using software or graphing tools. Compare the graph with the standard graph of potential parent functions to confirm your identification.

Here are a few examples to illustrate these steps:

Example 1: $<span$
Finding the parent function from an equation involves identifying the basic function that serves as a starting point for transformations. The parent function is typically a simple, standard function that undergoes transformations to create more complex functions. Here are general steps to find the parent function from an equation:
1. Identify the Key Elements:
  - Look for key elements in the equation, such as constants, coefficients, and exponents. These elements provide information about the specific features and transformations applied to the parent function.
2. Isolate the Transformations:
  - Separate the transformations applied to the parent function from the rest of the equation. This involves recognizing changes in the form of the equation that indicate shifts, stretches, compressions, or reflections.
3. Understand Common Parent Functions:
  - Familiarize yourself with common parent functions and their general forms. Some examples of parent functions include linear functions (y = x), quadratic functions (y = x^2), cubic functions (y = x^3), absolute value functions (y = |x|), square root functions (y = √x), and reciprocal functions (y = 1/x).
4. Identify the Specific Function:
  - Determine which parent function corresponds to the transformations indicated in the equation. For example, if the equation involves squaring (x^2), it may be related to a quadratic parent function.
5. Check for Additional Transformations:
  - Some equations may include multiple transformations. Check for additional elements in the equation that indicate shifts along the x-axis or y-axis, changes in amplitude, or reflections.
6. Verify with Graphs:
  - Plot the graph of the equation using software or graphing tools. Compare the graph with the standard graph of potential parent functions to confirm your identification.
Here are a few examples to illustrate these steps:
- Example 1: $y = 2x + 3$
  - This equation represents a linear function (y = x) with a slope of 2 and a y-intercept of 3. Therefore, the parent function is $y = x$ .
- Example 2: $y = 4x^2 - 1$
  - This equation represents a quadratic function with a vertical stretch by a factor of 4 and a vertical shift downward by 1. The parent function is $y = x^2$ .
- Example 3: $y = -\sqrt{2x}$
  - This equation represents a square root function with a reflection across the x-axis and a horizontal compression by a factor of 2. The parent function is $y = \sqrt{x}$ .
By analyzing the equation and recognizing the specific transformations applied, you can identify the parent function that serves as the foundation for those transformations.
class="katex"> $y = 2x + 3$ y=2x+3
- This equation represents a linear function (y = x) with a slope of 2 and a y-intercept of 3. Therefore, the parent function is $y = x$ .
Example 2: $y = 4x^2 - 1$
- This equation represents a quadratic function with a vertical stretch by a factor of 4 and a vertical shift downward by 1. The parent function is $y = x^2$ .
Example 3: $y = -\sqrt{2x}$
- This equation represents a square root function with a reflection across the x-axis and a horizontal compression by a factor of 2. The parent function is $y = \sqrt{x}$ .

By analyzing the equation and recognizing the specific transformations applied, you can identify the parent function that serves as the foundation for those transformations.

Sure, here is a comprehensive explanation of determining the parent function from an equation or graph:

How to determine the parent function from an equation or graph?

Identifying the parent function from an equation or graph involves analyzing the basic form of the function and recognizing the transformations that have been applied to it.

For equations:

Simplify the equation: Remove any unnecessary constants or coefficients and express the equation in its simplest form.
Recognize the basic function type: Identify the type of function represented by the equation, such as linear, quadratic, exponential, or trigonometric.
Identify transformations: Compare the simplified equation to the standard form of the basic function type. Transformations may include horizontal shifts, vertical shifts, stretches, or reflections.
Reverse transformations: Apply the inverse operations of the transformations to the simplified equation to obtain the parent function. For example, if the function is shifted 2 units to the right, shift it 2 units to the left.

For graphs:

Identify the basic shape: Observe the overall shape of the graph and determine the basic function type it resembles, such as a straight line, parabola, or sine wave.
Analyze transformations: Look for any deviations from the basic shape that indicate transformations. For instance, if the graph is shifted vertically, it suggests a vertical shift.
Reverse transformations: Mentally reverse the transformations to visualize the graph of the parent function. For example, if the graph is shifted 3 units upward, imagine the graph moving 3 units downward.
Match the graph to the parent function: Compare the visualized graph to the standard graph of the basic function type to identify the parent function.

What characteristics signify the parent function in mathematical equations or graphs?

The parent function represents the most basic form of a mathematical family or category. It exhibits the fundamental properties and characteristics of that function type.

In equations:

Simplicity: The parent function is the simplest expression of the function type, free from unnecessary constants or coefficients.
Standard form: The parent function adheres to the standard form of its function type, such as y = x for linear functions or y = x^2 for quadratic functions.

In graphs:

Basic shape: The graph of the parent function exhibits the essential shape of its function type, such as a straight line for linear functions or a parabola for quadratic functions.
Symmetry: The graph of the parent function may exhibit symmetry properties, such as reflection across the y-axis for even functions or reflection across the x-axis for odd functions.

Are there patterns or indicators that help identify the parent function?

Yes, there are several patterns and indicators that can help identify the parent function in equations or graphs:

Degree of the polynomial: The degree of the polynomial in an equation corresponds to the basic shape of its graph. For instance, a first-degree polynomial results in a linear graph, while a second-degree polynomial corresponds to a parabolic graph.
Intercepts: The intercepts of a graph, such as the x-intercept and y-intercept, provide clues about the parent function. For example, a linear function has a single x-intercept and a y-intercept.
End behavior: The behavior of the graph as x approaches positive or negative infinity can indicate the parent function. For instance, a quadratic function approaches positive or negative infinity as x approaches positive or negative infinity, respectively.

Can transformations in equations or graphs reveal the parent function?

Transformations in equations or graphs provide valuable information about the parent function. By reversing the transformations, one can uncover the basic form of the function.

Horizontal shifts: Horizontal shifts move the graph of the function sideways without affecting its shape.
Vertical shifts: Vertical shifts move the graph of the function up or down without altering its shape.
Stretching and compressing: Stretching or compressing the graph changes its width or height while maintaining its overall shape.
Reflections: Reflecting the graph across the x-axis or y-axis changes the sign of the function.

How do different mathematical families or categories relate to their parent functions?

Different mathematical families or categories share a common parent function, which represents the basic form of that group of functions. Each member of the family is derived from the parent function by applying various transformations.

For example, the family of linear functions has y = x as its parent function. Other linear functions, such as y = x + 2,