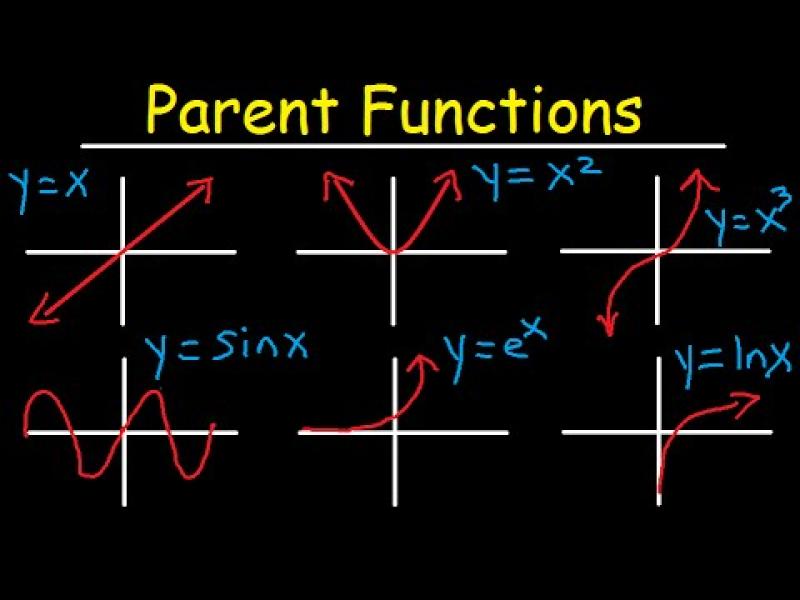
Function Foundations: How to Find Parent Functions

_{November 19, 2023 by JoyAnswer.org, Category : Mathematics}

How to find parent functions? Explore the fundamentals of parent functions and learn how to identify them with this guide. Gain insights into recognizing key characteristics that define parent functions.

How to find parent functions?

Parent functions are fundamental functions that serve as the base or template for a family of functions. These functions typically represent the simplest form of a particular type of function and serve as a reference point for understanding how different transformations affect graphs.

Here are some common parent functions:

Linear Function: $f(x) = x$
Quadratic Function: $f(x) = x^2$
Cubic Function: $f(x) = x^3$
Square Root Function: $f(x) = \sqrt{x}$
Absolute Value Function: $f(x) = |x|$
Exponential Function: $f(x) = a^x$ (where $a$ is a constant)
Logarithmic Function: $f(x) = \log_a(x)$ (where $a$ is a constant)

To understand how transformations affect functions, it's important to grasp these basic functions first. From there, transformations such as shifting, stretching, compressing, and reflecting can be applied to these parent functions to create more complex graphs.

For instance, if you take the parent function $f(x) = x^2$ and apply a transformation like $f(x) = (x - 2)^2 + 3$ , it will shift the graph 2 units to the right and 3 units upward compared to the basic $x^2$ function.

Understanding parent functions helps in recognizing patterns and behaviors across different functions and makes it easier to analyze and graph more complex functions.

1. Methods or Resources for Identifying Parent Functions in Mathematics

Several methods and resources can aid in identifying parent functions in mathematics. These include:

Understanding the Definition of a Parent Function: A parent function is the simplest form of a family of functions. It is the basic function from which all other functions in the family are derived through transformations.
Recognizing Common Parent Functions: Familiarize yourself with the basic parent functions, such as linear, quadratic, cubic, exponential, logarithmic, and trigonometric functions.
Analyzing Function Rules: Examine the function rule to determine the type of function it represents. For instance, a function represented by y = mx + b is a linear function, while y = x^2 is a quadratic function.
Identifying Transformations: Recognize transformations applied to parent functions. These transformations include horizontal and vertical shifts, reflections, and stretching or shrinking.
Utilizing Visual Representations: Graph the function to observe its shape and characteristics. Parent functions typically have distinct shapes that can aid in identification.
Employing Reference Materials: Refer to textbooks, online resources, and mathematical software to gain a deeper understanding of parent functions and their transformations.

2. Role of Mathematical Patterns and Structures

Mathematical patterns and structures play a significant role in recognizing parent functions. By understanding the patterns and structures of parent functions, one can more easily identify them and distinguish them from derived functions.

Patterns in Function Rules: Parent functions often exhibit consistent patterns in their function rules. For example, linear functions have a constant slope, while quadratic functions have a parabolic shape.
Structures of Parent Functions: The structures of parent functions govern their behavior and transformations. Understanding these structures allows for the prediction of how a parent function will be affected by transformations.
Similarity Among Function Families: Recognizing the similarities among functions within a family helps in identifying parent functions. For instance, all exponential functions share the same basic exponential structure, regardless of their transformations.

3. Distinguishing Parent Functions from Derived Functions

Common characteristics distinguish parent functions from derived functions:

Simplicity: Parent functions are the simplest forms of their respective families, lacking any transformations.
Basic Function Rules: Parent functions have basic function rules that represent their fundamental behavior.
Distinct Shapes: Parent functions typically have distinct graphical representations, such as the straight line of a linear function or the parabola of a quadratic function.
Originality: Parent functions serve as the original functions from which derived functions are obtained through transformations.

4. Graphical Representations for Identifying Parent Functions

Graphical representations can be powerful tools for visualizing and identifying parent functions. By observing the shape, features, and behavior of a function graph, one can often determine its parent function.

Characteristic Shapes: Parent functions have distinct graphical shapes that set them apart from other functions. For instance, linear functions exhibit a straight line graph, while quadratic functions have a parabolic graph.
End Behavior: The end behavior of a function, or its behavior as the input approaches positive or negative infinity, often provides clues about its parent function. For example, linear functions have constant end behavior, while quadratic functions have a parabolic end behavior.
Symmetry: The presence or absence of symmetry in a function's graph can also aid in identification. For instance, even functions have symmetric graphs about the y-axis, while odd functions have symmetric graphs about the origin.

5. Teaching Students to Identify and Understand Parent Functions

Educators can effectively teach students to identify and understand parent functions by employing various strategies:

Clear Definition and Examples: Provide a clear definition of parent functions and illustrate with concrete examples.
Exploration of Function Families: Guide students through the exploration of different function families, emphasizing the similarities and differences between parent functions and their derived counterparts.
Analysis of Function Rules and Transformations: Encourage students to analyze function rules to identify the parent function and recognize the transformations applied to it.
Utilization of Graphical Representations: Emphasize the importance of graphical representations in visualizing and identifying parent functions. Engage students in analyzing function graphs and relating them to their parent functions.
Active Learning and Practice: Employ active learning techniques, such as group work, problem-solving exercises, and interactive simulations, to help students solidify their understanding of parent functions.