Calculating the Critical Value of a Z-Score: Statistical Analysis
October 2, 2023 by JoyAnswer.org, Category : Mathematics
How do you calculate critical value of z score? Learn how to calculate the critical value of a Z-score for statistical analysis and hypothesis testing, with a focus on significance levels.
- 1. How do you calculate critical value of z score?
- 2. Calculating Critical Value of Z-Score: A Statistical Guide.
- 3. Statistical Significance: How to Calculate the Critical Value of Z.
- 4. Z-Scores and Critical Values: The Mathematics Behind Significance.
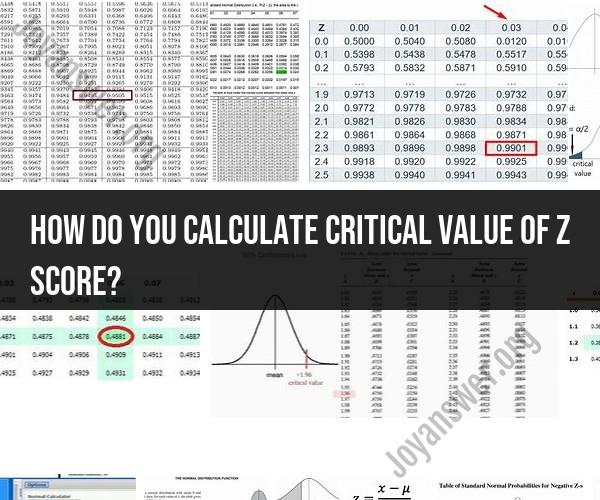
How do you calculate critical value of z score?
The critical value of a z-score is the value on the standard normal distribution (z-distribution) beyond which a specified percentage of data falls. It is often used in hypothesis testing and confidence interval calculations in statistics. To calculate the critical value of a z-score, you need to know the desired level of significance (alpha) and whether you're conducting a one-tailed or two-tailed test. Here are the steps:
Determine the Significance Level (Alpha):
- Alpha (α) is the probability of making a Type I error (rejecting a true null hypothesis). It is typically set by the researcher based on the level of confidence desired. Common values for alpha include 0.05 (5%) and 0.01 (1%).
Identify the Type of Test:
- Determine whether you are conducting a one-tailed or two-tailed test. This is based on the nature of your hypothesis and the research question. A one-tailed test tests a specific direction (e.g., greater than or less than), while a two-tailed test is more general.
Look Up Critical Values in a Z-Table or Use a Calculator:
- To find the critical value, you can consult a standard normal distribution table (z-table) or use a calculator or statistical software. The table provides critical values corresponding to various levels of significance and types of tests.
- For a one-tailed test, you need to find the z-score associated with the desired level of significance (α) in the appropriate tail (either left or right).
- For a two-tailed test, you need to find two critical values: one for α/2 in the left tail and one for α/2 in the right tail.
Calculate the Critical Value:
- Multiply the z-score you found in the z-table by -1 if you're dealing with the left tail (for one-tailed tests) or the right tail (for two-tailed tests). This ensures that you have the correct direction for the critical value.
- For two-tailed tests, you'll have two critical values, one for each tail.
Here's an example:
Suppose you're conducting a two-tailed hypothesis test with a significance level (α) of 0.05. You need to find the critical values for a standard normal distribution.
α/2 = 0.05/2 = 0.025 (for each tail).
Look up the z-score associated with a cumulative probability of 0.025 in a z-table. You'll find that it's approximately -1.96 for the left tail and 1.96 for the right tail.
So, for this two-tailed test at a 0.05 significance level, the critical values are -1.96 and 1.96.
These critical values are used to determine the rejection region(s) in hypothesis testing. If your calculated z-score falls outside the range defined by these critical values, you would reject the null hypothesis. If it falls within the range, you would fail to reject the null hypothesis.
Calculating Critical Value of Z-Score: A Statistical Guide
The critical value of a z-score is the value that separates the rejection region from the non-rejection region. The rejection region is the area under the normal curve where the null hypothesis is rejected. The non-rejection region is the area under the normal curve where the null hypothesis is not rejected.
To calculate the critical value of a z-score, you need to know the significance level (α). The significance level is the probability of rejecting the null hypothesis when it is true. The most common significance levels are 0.05 and 0.01.
Once you know the significance level, you can look up the critical value of the z-score in a z-table. A z-table is a table that shows the probability of obtaining a z-score of a certain value or greater.
Here is an example of how to calculate the critical value of a z-score:
Suppose you are conducting a hypothesis test and the significance level is 0.05. You want to calculate the critical value of the z-score for a two-tailed test.
To do this, you would look up the value 0.025 in the z-table. The value 0.025 is the probability of obtaining a z-score of 1.96 or greater in one tail of the normal curve. Since the test is two-tailed, you need to double this value to get the critical value of the z-score.
Therefore, the critical value of the z-score for a two-tailed test with a significance level of 0.05 is 1.96.
Statistical Significance: How to Calculate the Critical Value of Z
The critical value of z is used to determine the statistical significance of a hypothesis test. A hypothesis test is a statistical procedure that is used to test a claim about a population parameter.
To conduct a hypothesis test, you first need to formulate a null hypothesis and an alternative hypothesis. The null hypothesis is the claim that you are testing. The alternative hypothesis is the claim that you are making if the null hypothesis is rejected.
Once you have formulated your hypotheses, you need to collect a sample of data from the population of interest. You then need to calculate a test statistic. The test statistic is a statistic that is calculated from the sample data and that is used to test the null hypothesis.
The next step is to calculate the p-value. The p-value is the probability of obtaining a test statistic as extreme as the one that was calculated, assuming that the null hypothesis is true.
If the p-value is less than the significance level, then the null hypothesis is rejected. This means that there is enough evidence to support the alternative hypothesis.
If the p-value is not less than the significance level, then the null hypothesis is not rejected. This does not necessarily mean that the null hypothesis is true. It simply means that there is not enough evidence to reject the null hypothesis.
Z-Scores and Critical Values: The Mathematics Behind Significance
The mathematical relationship between z-scores and critical values is based on the normal distribution. The normal distribution is a bell-shaped curve that is symmetrical around the mean.
The z-score is a measure of how many standard deviations a particular value is away from the mean. The critical value is the z-score that separates the rejection region from the non-rejection region.
The rejection region is the area under the normal curve where the null hypothesis is rejected. The non-rejection region is the area under the normal curve where the null hypothesis is not rejected.
The significance level is the probability of rejecting the null hypothesis when it is true. The critical value is chosen so that the probability of rejecting the null hypothesis when it is true is equal to the significance level.
For example, if the significance level is 0.05, then the critical value is chosen so that the probability of rejecting the null hypothesis when it is true is 0.05. This means that there is a 5% chance of making a Type I error, which is the error of rejecting the null hypothesis when it is true.
Z-scores and critical values are used in a variety of statistical tests, including the z-test, the t-test, and the chi-square test. These tests are used to test a variety of claims about population parameters, such as the mean, the variance, and the proportion.
