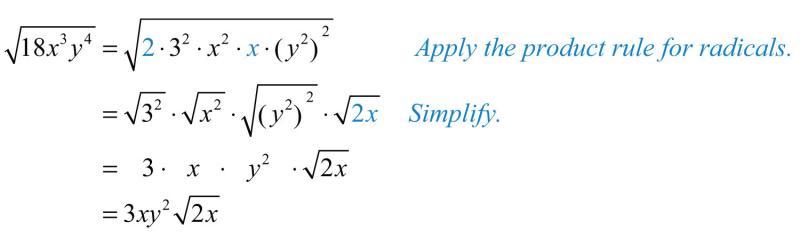Writing in Radical Form: Mathematical Notation Guidelines

_{December 7, 2023 by JoyAnswer.org, Category : Mathematics}

How do you write radical form? Understand the principles behind writing expressions in radical form. Learn the guidelines and conventions for presenting mathematical equations in radical notation.

How do you write radical form?

Writing in radical form involves expressing expressions with roots and exponents using the radical symbol (√) or nth root (∛, ∜) notation. Here are guidelines for writing expressions in radical form:

Square Root (√): The square root (√) represents the second root of a number or expression. To write an expression in square root form:
- Use the radical symbol (√) followed by the expression under the radical sign. For example: √(x), √(9), √(a^2).
nth Root (∛, ∜): The nth root (∛ for cube root, ∜ for fourth root, etc.) represents the radical form for any positive integer 'n.' To write an expression in nth root form:
- Use the radical symbol (∛, ∜) with the value of 'n' outside the radical and the expression under the radical. For example: ∛(x), ∛(27), ∜(b^3).
Fractional Exponents: Expressing exponents in radical form involves using fractional exponents. For instance:
- $x^{\frac{1}{n}}$ represents the nth root of 'x.' It is equivalent to the radical form ∛(x), ∜(x), etc., depending on the value of 'n.'

Here are some examples to illustrate:

$x^{\frac{1}{2}}$ is equivalent to √(x) and represents the square root of 'x.'
$y^{\frac{1}{3}}$ is equivalent to ∛(y) and represents the cube root of 'y.'
$z^{\frac{1}{4}}$ is equivalent to ∜(z) and represents the fourth root of 'z.'

When converting from exponent notation to radical form, the denominator of the fractional exponent indicates the root (radical), and the numerator represents the power to which the expression is raised.

Expressing expressions in radical form is useful for simplifying and understanding roots and fractional exponents, especially when dealing with calculations involving powers and radicals.

What constitutes the process of expressing a mathematical expression in radical form?

Expressing a mathematical expression in radical form involves rewriting it using radicals and exponents to represent roots. Here's a breakdown of the process:

1. Identify relevant expressions: Look for expressions containing roots (square root, cube root, etc.) or fractional/negative exponents.2. Factor and simplify: Before converting, simplify the expression by factoring the radicands (numbers under the radical symbol) and extracting perfect squares, cubes, or higher-order powers.3. Apply exponent rules: Remember that exponents inside a radical can be distributed and simplified according to their rules.4. Convert fractional exponents to radicals: For fractional exponents, apply the formula: x^(n/m) = n√(x^m).5. Convert negative exponents to radicals: For negative exponents, apply the formula: x^(-n) = 1/n√(x^n).6. Combine like terms: Group all radicals with the same index (e.g., all square roots) and simplify by combining coefficients.7. Rationalize denominators: If denominators contain radicals, eliminate them by multiplying both numerator and denominator by the appropriate conjugate (a term obtained by rationalizing the denominator).8. Simplify further: Look for any remaining simplification opportunities, such as combining radicals with the same radicand and simplifying fractions.

Here are some additional points to remember:

This process is only applicable for positive integer exponents when converting to radical form.

Negative and fractional exponents require different approaches to express them in radical form.

The order of operations (PEMDAS) applies during the conversion process.

Practice and understanding of basic algebraic rules are crucial for successful conversion.

By following these steps and rules, you can effectively express mathematical expressions in radical form, facilitating further analysis and simplification.