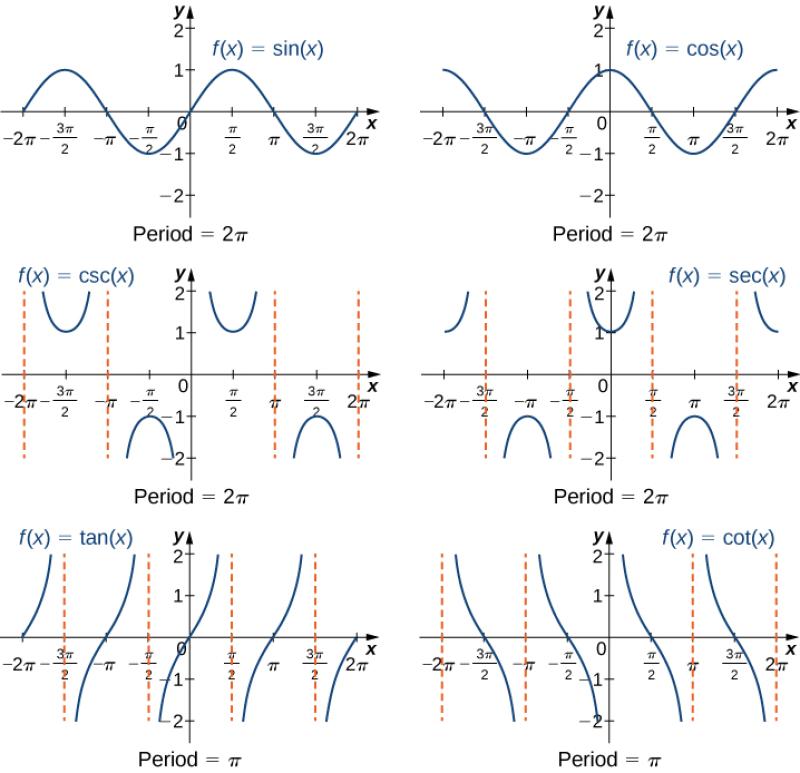
Unveiling the Six Trig Functions: A Comprehensive Overview

_{November 17, 2023 by JoyAnswer.org, Category : Mathematics}

What are the six trig functions? Delve into the world of trigonometry as this guide unveils the six fundamental trigonometric functions. Understand their definitions and relationships, empowering your mastery of trigonometric concepts.

Table of Contents

What are the six trig functions?

The six trigonometric functions are derived from the ratios of the sides of a right triangle. These functions are commonly denoted as sin, cos, tan, cosec, sec, and cot. Each trigonometric function is associated with a specific angle in a right triangle. Here is a comprehensive overview of the six trigonometric functions:

Sine Function (sin θ):
- Definition: In a right triangle, the sine of an angle ( $θ$ ) is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Formula: $\sin θ = \frac{{\text{{opposite side}}}}{{\text{{hypotenuse}}}}$
Cosine Function (cos θ):
- Definition: The cosine of an angle ( $θ$ ) is the ratio of the length of the adjacent side to the length of the hypotenuse in a right triangle.
- Formula: $\cos θ = \frac{{\text{{adjacent side}}}}{{\text{{hypotenuse}}}}$
Tangent Function (tan θ):
- Definition: The tangent of an angle ( $θ$ ) is the ratio of the length of the side opposite the angle to the length of the adjacent side.
- Formula: $\tan θ = \frac{{\text{{opposite side}}}}{{\text{{adjacent side}}}}$
Cosecant Function (csc θ):
- Definition: The cosecant of an angle ( $θ$ ) is the reciprocal of the sine. It is the ratio of the hypotenuse to the side opposite the angle.
- Formula: $\csc θ = \frac{1}{{\sin θ}}$
Secant Function (sec θ):
- Definition: The secant of an angle ( $θ$ ) is the reciprocal of the cosine. It is the ratio of the hypotenuse to the adjacent side.
- Formula: $\sec θ = \frac{1}{{\cos θ}}$
Cotangent Function (cot θ):
- Definition: The cotangent of an angle ( $θ$ ) is the reciprocal of the tangent. It is the ratio of the adjacent side to the side opposite the angle.
- Formula: $\cot θ = \frac{1}{{\tan θ}}$

These trigonometric functions are fundamental in trigonometry and are widely used in various mathematical and scientific applications. They provide a way to relate the angles of a right triangle to the lengths of its sides and are essential in solving problems involving angles, distances, and periodic phenomena. The functions can also be defined using the unit circle, providing a more general representation beyond right triangles.

Certainly, here's a comprehensive explanation of the six primary trigonometric functions:

List and define the six primary trigonometric functions:

The six primary trigonometric functions, also known as the fundamental trigonometric functions, are:

Sine (sin): The sine function represents the ratio of the opposite side to the hypotenuse of a right triangle. It is denoted by sin(θ), where θ is the angle measured from the adjacent side.
Cosine (cos): The cosine function represents the ratio of the adjacent side to the hypotenuse of a right triangle. It is denoted by cos(θ), where θ is the angle measured from the adjacent side.
Tangent (tan): The tangent function represents the ratio of the opposite side to the adjacent side of a right triangle. It is denoted by tan(θ), where θ is the angle measured from the adjacent side.
Cotangent (cot): The cotangent function is the reciprocal of the tangent function. It is denoted by cot(θ), where θ is the angle measured from the adjacent side.
Secant (sec): The secant function is the reciprocal of the cosine function. It is denoted by sec(θ), where θ is the angle measured from the adjacent side.
Cosecant (csc): The cosecant function is the reciprocal of the sine function. It is denoted by csc(θ), where θ is the angle measured from the adjacent side.

2. What constitute the six core trigonometric functions and their properties:

The six core trigonometric functions are the building blocks of trigonometry. They have several fundamental properties, including:

Periodicity: Trigonometric functions are periodic, meaning their values repeat after a certain interval. For sine and cosine functions, the period is 2π radians or 360 degrees.
Amplitude: The amplitude of a trigonometric function is the maximum distance between its graph and the midline (x-axis). For sine and cosine functions, the amplitude is 1.
Midline: The midline of a trigonometric function is the horizontal line about which its graph oscillates. For sine and cosine functions, the midline is y = 0.
Symmetry: Trigonometric functions exhibit various symmetry properties. For instance, sine and cosine functions are even functions, while tangent and cotangent functions are odd functions.

3. How do the six trigonometric functions relate to angles and sides in trigonometry:

Trigonometric functions are defined in terms of angles and sides of right triangles. They provide a way to calculate the unknown sides or angles of a triangle given other known values. The relationships between angles and sides are expressed through trigonometric identities, such as the Pythagorean theorem and the law of sines and cosines.

Here's a summary of how each trigonometric function relates to angles and sides: