Formula for Interval Notation: Expressing Ranges Mathematically

_{November 15, 2023 by JoyAnswer.org, Category : Mathematics}

What is the formula for interval notation? Understand the formula for interval notation, which is used to express ranges mathematically. This guide provides insights into representing intervals using a concise mathematical notation.

Table of Contents

What is the formula for interval notation?

Interval notation is a way to express a range of real numbers using parentheses, brackets, and infinity symbols. The basic forms of interval notation are:

Open Interval:
- $(a, b)$ represents all real numbers $x$ such that $a < x < b$ .
Closed Interval:
- $[a, b]$ represents all real numbers $x$ such that $a \leq x \leq b$ .
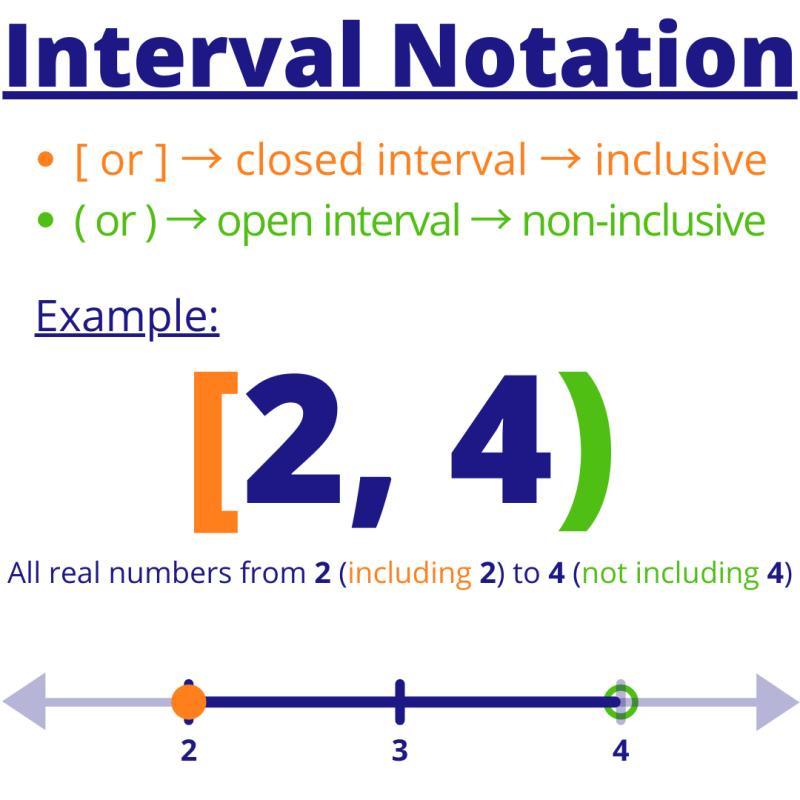
Half-Open or Half-Closed Intervals:
- These intervals have one endpoint included and one excluded or vice versa. For example, $[a, b)$ includes $a$ but excludes $b$ .
Infinite Intervals:
- $(-\infty, a)$ represents all real numbers less than $a$ .
- $(a, \infty)$ represents all real numbers greater than $a$ .
- $(-\infty, \infty)$ represents all real numbers.

The general formula for expressing an interval $(a, b)$ is:

$a < x < b$

And for a closed interval $[a, b]$ :

$a \leq x \leq b$

In these formulas, $a$ and $b$ are real numbers, and $x$ is the variable representing the range of numbers.

Here are a few examples of interval notation:

The interval of all real numbers greater than 2: $(2, \infty)$
The interval of all real numbers less than or equal to 5: $(-\infty, 5]$
The interval of all real numbers between -3 and 3 (including -3 and 3): $[-3, 3]$
The interval of all real numbers greater than -1 but less than 4: $(-1, 4)$

When working with inequalities and expressing ranges, interval notation provides a concise and standardized way to communicate sets of numbers.

What is the formula used for interval notation in mathematics?

Interval notation is a way of representing sets of real numbers using brackets, parentheses, and numbers. The formula for interval notation is as follows:

[a, b]

This notation represents the set of all real numbers between and including a and b. The left bracket indicates that a is included in the interval, and the right bracket indicates that b is included in the interval.

Example: The interval [2, 5] represents the set of all real numbers between 2 and 5, including 2 and 5.

How is interval notation applied to represent sets of real numbers?

Interval notation can be used to represent a variety of sets of real numbers, including:

Closed intervals: A closed interval is a set of real numbers that includes both endpoints. For example, the interval [2, 5] is a closed interval.
Open intervals: An open interval is a set of real numbers that excludes both endpoints. For example, the interval (2, 5) is an open interval.
Half-closed intervals: A half-closed interval is a set of real numbers that includes one endpoint and excludes the other. For example, the interval [2, 5) is a half-closed interval, and the interval (2, 5] is another half-closed interval.
Infinite intervals: Interval notation can also be used to represent infinite sets of real numbers. For example, the interval (-∞, ∞) represents the set of all real numbers.

Example: The interval [−3, 1) represents the set of all real numbers between −3 and 1, including −3 but not including 1.

Are there conventions or rules to follow when using interval notation?

Yes, there are a few conventions or rules to follow when using interval notation:

The endpoints of an interval must be real numbers.
The left endpoint of an interval must be less than or equal to the right endpoint.
The parentheses and brackets used to represent an interval have different meanings:
- Brackets [ ] indicate that the endpoint is included in the interval.
- Parentheses ( ) indicate that the endpoint is excluded from the interval.

Can interval notation represent infinite sets or intervals?

Yes, interval notation can be used to represent infinite sets or intervals. For example, the interval (-∞, ∞) represents the set of all real numbers, and the interval (0, ∞) represents the set of all positive real numbers.

How does interval notation simplify the representation of mathematical intervals?

Interval notation provides a concise and clear way to represent sets of real numbers. It is often more convenient than writing out a complete list of all the numbers in an interval. Interval notation is also useful for defining functions and for describing mathematical concepts such as continuity and limits.