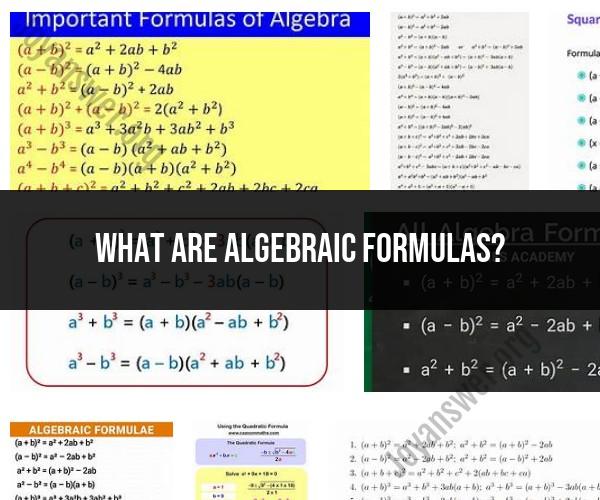
Demystifying Algebraic Formulas: Mathematical Expressions

_{September 26, 2023 by JoyAnswer.org, Category : Mathematics}

What are algebraic formulas? Gain an understanding of algebraic formulas and how they are used to represent mathematical relationships and solve equations.

Table of Contents

What are algebraic formulas?

Algebraic formulas, also known as algebraic expressions or mathematical expressions, are mathematical statements that represent relationships between variables and constants using algebraic operations. These expressions can be as simple as a single variable or complex combinations of variables, constants, and operations like addition, subtraction, multiplication, division, exponentiation, and more.

Here are some key components and examples of algebraic formulas:

Variables: Variables are symbols that represent unknown or changing values. Commonly used variables include "x," "y," and "z," although any letter or symbol can be used. For example, in the formula "2x + 3," "x" is a variable.
Constants: Constants are fixed numerical values that do not change within the context of the formula. For example, in the formula "3y - 7," "3" and "7" are constants.
Operations: Algebraic formulas involve mathematical operations like addition (+), subtraction (-), multiplication (*), division (/), exponentiation (^ or **), and more. For example:
- "3x + 2y" involves addition.
- "4a - 5b" involves subtraction.
- "2c * 7d" involves multiplication.
- "x / 2" involves division.
- "y^2" involves exponentiation.
Coefficients: Coefficients are constants that multiply variables in an expression. In the formula "4x," "4" is the coefficient of "x."
Terms: In algebraic expressions, terms are individual components separated by addition or subtraction signs. For example, in "3x + 2y - 7," "3x," "2y," and "-7" are terms.
Parentheses: Parentheses are used to indicate the order of operations within an expression. For instance, "(2x + 3)" means that you must perform the addition inside the parentheses before any multiplication or other operations outside the parentheses.

Algebraic formulas are used extensively in mathematics to describe relationships, solve equations, and model real-world situations. They serve as a foundation for various mathematical concepts, including solving equations, graphing functions, and performing calculations in areas such as physics, engineering, economics, and more. Understanding algebraic formulas is essential for solving mathematical problems and analyzing quantitative data.

The three titles you have provided highlight the importance of understanding and using algebraic formulas. Algebraic formulas are mathematical equations that can be used to solve a variety of problems. By understanding and using algebraic formulas, students can improve their problem-solving skills and become more proficient in mathematics.

Demystifying Algebraic Formulas: What They Are and How to Use Them

This title emphasizes the fact that algebraic formulas are not as mysterious as they may seem. With a little understanding of the underlying concepts, students can learn to use algebraic formulas effectively.

Algebraic Formulas Unveiled: A Comprehensive Overview

This title highlights the wide range of algebraic formulas that are available. Students can use these formulas to solve a variety of problems, such as finding the area of a triangle, the slope of a line, or the volume of a sphere.

Algebra Essentials: Understanding and Applying Formulas

This title emphasizes the importance of understanding how to apply algebraic formulas. Students should not simply memorize algebraic formulas; they should also understand what the formulas mean and how to use them to solve problems.

Here are some tips for understanding and using algebraic formulas:

Understand the underlying concepts. Algebraic formulas are based on a few fundamental concepts, such as variables, constants, and operations. By understanding these concepts, students can better understand how to use algebraic formulas.
Memorize the basic formulas. There are a few basic algebraic formulas that students should memorize. These formulas can be used to solve a variety of problems.
Practice using the formulas. The best way to learn how to use algebraic formulas is to practice using them. Students can find practice problems in textbooks, online resources, and workbooks.
Check your work. Make sure that your answers are correct by using other methods, such as graphing or numerical methods.

Algebraic formulas can be a powerful tool for solving mathematical problems. By understanding and using algebraic formulas effectively, students can improve their problem-solving skills and become more proficient in mathematics.