Finding Slope Through Each Pair of Points: Systematic Approach

_{November 15, 2023 by JoyAnswer.org, Category : Mathematics}

How to find the slope through each pair of points? Master the systematic approach to finding the slope through each pair of points. This guide provides clear instructions on calculating the slope for multiple point pairs on a graph.

Table of Contents

How to find the slope through each pair of points?

If you have a set of points and you want to find the slope for each pair of points systematically, you can follow these steps:

Identify the Pairs of Points:
- If you have $n$ points, there will be $\frac{n \cdot (n-1)}{2}$ unique pairs of points. Identify all these pairs.
Use the Slope Formula:
- The slope ( $m$ ) between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by: $m = \frac{{y_2 - y_1}}{{x_2 - x_1}}$
Calculate the Slope for Each Pair:
- For each pair of points, substitute the coordinates into the slope formula and calculate the slope. Repeat this process for all pairs.
Record the Results:
- Create a table or list to record the slopes corresponding to each pair of points. Ensure you label each slope with the corresponding pair of points.
Verify for Consistency:
- Check the results for consistency and accuracy. Ensure that the calculations are correct and that you haven't missed any pairs of points.

Here's a more detailed example:

Suppose you have three points: $A(1, 3)$ , $B(2, 7)$ , and $C(4, 11)$ .

Pairs of points are: $AB$ , $AC$ , and $BC$ .

For $AB$ : $m_{AB} = \frac{{7 - 3}}{{2 - 1}} = 4$
For $AC$ : $m_{AC} = \frac{{11 - 3}}{{4 - 1}} = 2.67$
For $BC$ : $m_{BC} = \frac{{11 - 7}}{{4 - 2}} = 2$

Record the results in a table:

$\begin{array}{|c|c|} \hline \text{Pair of Points} & \text{Slope} \\ \hline AB & 4 \\ \hline AC & 2.67 \\ \hline BC & 2 \\ \hline \end{array}$

This systematic approach ensures that you calculate the slope for each pair of points and organize the results for further analysis.

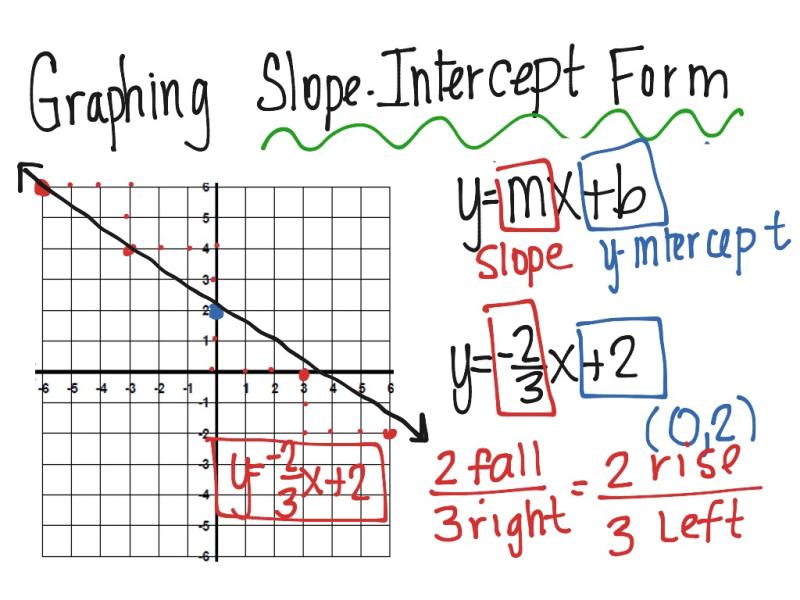
Geometry fundamentals: How to find the slope through each pair of points.

In geometry, slope is a measure of the steepness and direction of a line. It is calculated as the change in the y-coordinates of two points on the line divided by the change in their x-coordinates. The slope formula is:

slope = (y2 - y1) / (x2 - x1)

where (x1, y1) and (x2, y2) are the coordinates of the two points on the line.

Coordinates and connections: Identifying points for slope calculations.

To find the slope between two points, you need to know their coordinates. Coordinates are a system of numbers that specify the position of a point on a plane. In a two-dimensional coordinate system, the x-coordinate represents the horizontal position, and the y-coordinate represents the vertical position.

For example, the point (3, 4) is located three units to the right of the origin and four units up from the origin.

The slope formula: Step-by-step guide to determining slope between points.

To calculate the slope between two points, follow these steps:

Identify the coordinates of the two points.
Plug the coordinates into the slope formula.
Simplify the expression.

For example, to find the slope between the points (2, 1) and (5, 3), you would follow these steps:

Identify the coordinates: The coordinates of the first point are (2, 1) and the coordinates of the second point are (5, 3).
Plug the coordinates into the formula:

slope = (3 - 1) / (5 - 2)

Simplify:

slope = 2/3

Therefore, the slope between the points (2, 1) and (5, 3) is 2/3.

Graphical intuition: Visualizing slope on a coordinate plane.

Slope can be visualized on a coordinate plane. The slope of a line corresponds to its slant or steepness. A positive slope indicates that the line is slanted upwards from left to right, while a negative slope indicates that the line is slanted downwards from left to right. A slope of 0 indicates that the line is horizontal, and a slope that is undefined indicates that the line is vertical.

Real-world applications: Applying slope calculations in various contexts.

Slope has numerous applications in various fields, including:

Physics: Calculating velocity, acceleration, and other motion-related parameters.
Economics: Analyzing trends in financial markets and predicting price changes.
Engineering: Designing structures, such as bridges and buildings, to withstand certain loads and stresses.
Data analysis: Understanding relationships between variables and identifying patterns in datasets.

In conclusion, slope is a fundamental concept in geometry with a wide range of applications in real-world scenarios. By understanding the slope formula and its graphical representation, you can effectively calculate and interpret slope values, gaining valuable insights into the behavior of lines and their relationships in various contexts.