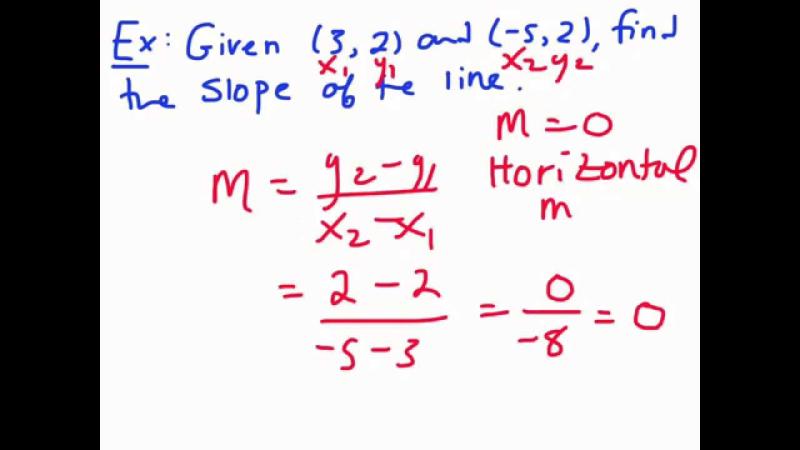How do you calculate slope when given two points?
To calculate the slope () between two points and , you can use the following formula:
Here's a step-by-step approach to calculating the slope:
Identify the Coordinates:
- Given two points, identify their coordinates. Let the coordinates of the first point be and the coordinates of the second point be .
Plug the Values into the Slope Formula:
- Substitute the coordinates into the slope formula:
Calculate the Numerator:
- Subtract the -coordinates of the two points: .
Calculate the Denominator:
- Subtract the -coordinates of the two points: .
Compute the Final Slope:
- Divide the result from step 3 by the result from step 4:
The resulting value is the slope of the line passing through the two given points. The slope represents the rate at which the -values change with respect to the -values. A positive slope indicates an upward trend, while a negative slope indicates a downward trend.
Keep in mind that if the denominator () is zero, the slope is undefined. This occurs when the two points have the same -coordinate, resulting in a vertical line.
This method provides a straightforward way to calculate the slope between two points on a graph or in a coordinate system.
Math mastery: How do you calculate slope when given two points?
The slope of a line is a measure of its steepness, indicating the direction and magnitude of its incline. It is calculated as the change in the y-coordinates of two points on the line divided by the change in their x-coordinates. The slope formula is:
slope = (y2 - y1) / (x2 - x1)
where (x1, y1) and (x2, y2) are the coordinates of the two points on the line.
Algebraic approach: Applying the slope formula to find the rate of change.
The slope formula is a powerful tool for analyzing linear relationships and understanding the rate of change between variables. It can be applied to a wide range of real-world scenarios, from determining the incline of a ramp to calculating the speed of a moving object.
For instance, consider a line representing the distance traveled by a car over time. The slope of this line would represent the car's constant speed. A positive slope indicates that the car is moving forward, while a negative slope indicates that it is moving backward. The steeper the slope, the faster the car is traveling.
Practical examples: Solving real-world problems with slope calculations.
Slope calculations have numerous applications in various fields, including:
Physics: Calculating velocity, acceleration, and other motion-related parameters.
Economics: Analyzing trends in financial markets and predicting price changes.
Engineering: Designing structures, such as bridges and buildings, to withstand certain loads and stresses.
Data analysis: Understanding relationships between variables and identifying patterns in datasets.
Additional considerations: Factoring in context for more meaningful slope interpretations.
When interpreting slope values, it is crucial to consider the context of the problem and the units of measurement. For example, the slope of a line representing population growth rate would be expressed in units of population increase per unit of time, such as people per year.
Additionally, the sign of the slope provides valuable information about the direction of change. A positive slope indicates an increase or a direct relationship, while a negative slope indicates a decrease or an inverse relationship.
Honing your skills: Practice exercises for calculating slope between two points.
To solidify your understanding of slope calculations, consider practicing with various exercises. These could involve:
Calculating the slope of lines given their coordinates.
Interpreting the significance of slope values in real-world scenarios.
Graphing lines based on their slope and intercepts.
Solving problems involving rate of change and linear relationships.
By consistently practicing with slope calculations, you can enhance your problem-solving skills, deepen your mathematical understanding, and gain confidence in applying these concepts to real-world situations.