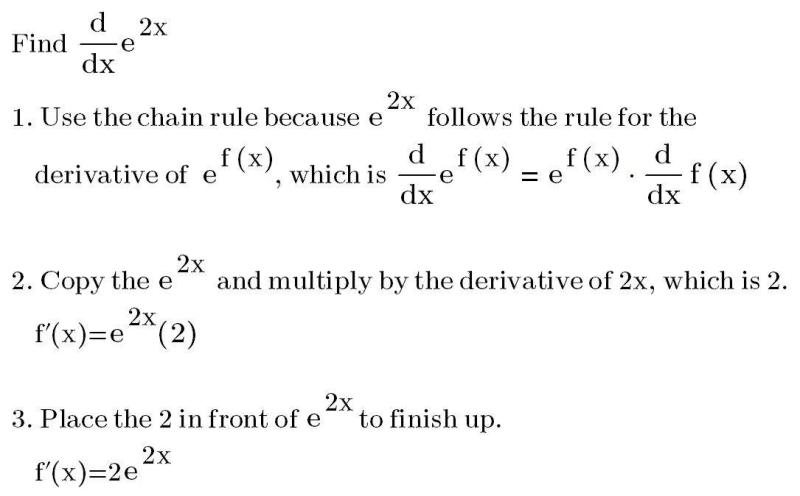Derivative of 'E': Calculus Techniques

Category: Mathematics

•

December 11, 2023

•

1 year ago

•

3 min read

•

1.9K Views

Share this article:

"How to take derivative of E? Explore the process of taking the derivative of the mathematical constant 'E'. This article provides insights into differentiating functions involving 'E' in calculus."

How to take derivative of E?

To find the derivative of the mathematical constant "e" raised to the power of a function, you can use the chain rule. The chain rule is a fundamental rule in calculus that allows you to find the derivative of a composite function.

If you have a function of the form $f(x) = e^{g(x)}$ , where $g(x)$ is a differentiable function, then the derivative $f'(x)$ is given by:

$f'(x) = e^{g(x)} \cdot g'(x)$

In words, the derivative of $e^{g(x)}$ is the original function $e^{g(x)}$ multiplied by the derivative of the exponent function $g(x)$ .

Here's a step-by-step breakdown:

Start with the original function: $f(x) = e^{g(x)}$
Identify the inner function $g(x)$ : $g(x)$
Find the derivative of the inner function $g'(x)$ .This is the derivative of $g(x)$ with respect to $x$ .
Multiply the original function by the derivative of the inner function: $f'(x) = e^{g(x)} \cdot g'(x)$

This rule is a direct application of the chain rule, which states that the derivative of a composition of functions is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function.

For example, if you have $f(x) = e^{2x}$ , where $g(x) = 2x$ , then the derivative $f'(x)$ would be: $f'(x) = e^{2x} \cdot 2$

It's important to note that the derivative of $e^x$ with respect to $x$ is simply $e^x$ .

How can the derivative of the variable "E" be calculated?

Unfortunately, your question is incomplete and lacks context to accurately answer how to calculate the derivative of the variable "E".

To accurately determine the derivative of "E", I need more information about the expression or function it represents. Please provide additional details such as:

The entire equation or expression containing "E": Knowing the full context of the equation is crucial to understand how "E" functions and how to differentiate it.