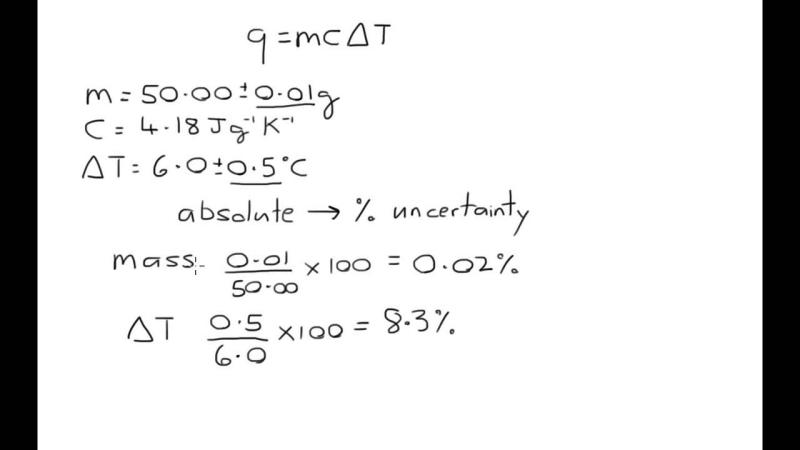Calculating Uncertainty in Density Determination

_{December 5, 2023 by JoyAnswer.org, Category : Science}

How to calculate the uncertainty in the calculated density? Learn how to calculate uncertainty in determined densities. This article provides methods and formulas to assess and quantify uncertainty in density calculations, offering insights into the precision of density measurements.

How to calculate the uncertainty in the calculated density?

Calculating the uncertainty in the determination of density involves considering the uncertainties associated with the measurements used in the calculation. The general formula for the uncertainty in a calculated quantity involving two or more measured values is given by the propagation of uncertainties. Here is the formula for the uncertainty in the density (ρ) calculation:

$\delta \rho = \rho \cdot \sqrt{\left(\frac{\delta m}{m}\right)^2 + \left(\frac{\delta V}{V}\right)^2}$

where:

$\delta \rho$ is the uncertainty in density,
$\rho$ is the calculated density,
$\delta m$ is the uncertainty in the mass measurement,
$m$ is the measured mass,
$\delta V$ is the uncertainty in the volume measurement,
$V$ is the measured volume.

Here are the steps to calculate the uncertainty in density:

Determine the Measured Mass ( $m$ ):
- Measure the mass of the object or substance using an appropriate scale or balance. Record the value as $m$ .
Determine the Uncertainty in Mass ( $\delta m$ ):
- Identify and quantify the sources of uncertainty in the mass measurement. This could include uncertainties in the instrument's precision, calibration, or other factors. Record the uncertainty as $\delta m$ .
Determine the Measured Volume ( $V$ ):
- Measure the volume of the object or substance using an appropriate instrument (e.g., graduated cylinder, burette, etc.). Record the value as $V$ .
Determine the Uncertainty in Volume ( $\delta V$ ):
- Identify and quantify the sources of uncertainty in the volume measurement. This may include uncertainties in the instrument's calibration, precision, or other factors. Record the uncertainty as $\delta V$ .
Calculate the Uncertainty in Density ( $\delta \rho$ ):
- Use the formula mentioned above to calculate the uncertainty in density.

It's crucial to note that the uncertainties ( $\delta m$ , $\delta V$ ) should be expressed as standard deviations or uncertainties at a specific confidence level (e.g., 95% confidence). If the uncertainties are given as absolute uncertainties (e.g., ±0.1 g), they should be divided by the corresponding measured values ( $m$ , $V$ ) to obtain relative uncertainties.

Remember that this method assumes that the uncertainties in mass and volume are independent and that there is no correlation between them. If there is a correlation, additional considerations may be needed in the uncertainty analysis.

How is uncertainty quantified when calculating density, and what factors contribute to this uncertainty?

There are several ways to quantify uncertainty when calculating density. Some common methods include:

Standard deviation: This is a measure of the variability of a set of data. It is calculated by taking the square root of the average of the squared differences from the mean.
Relative standard deviation: This is the standard deviation divided by the mean. It is a dimensionless quantity that expresses the uncertainty as a percentage of the mean.
Relative uncertainty: This is the absolute value of the difference between a measurement and the mean divided by the mean. It is also a dimensionless quantity that expresses the uncertainty as a percentage of the mean.

The choice of which method to use depends on the specific application. For example, if the density measurements are being used to compare different materials, then the relative standard deviation or relative uncertainty may be more appropriate. This is because these measures are not affected by the scale of the measurements.

In addition to the method used to quantify uncertainty, there are also a number of factors that can contribute to uncertainty in density measurements. These factors include:

Instrument error: All instruments have some degree of error. This error can be caused by a number of factors, such as calibration errors, noise, and drift.
Sampling error: When measuring the density of a material, it is important to take a representative sample. If the sample is not representative, then the density measurement will not be accurate.
Environmental factors: Environmental factors, such as temperature and pressure, can affect the density of a material. It is important to control these factors when measuring density.

By understanding the different methods of quantifying uncertainty and the factors that can contribute to uncertainty, it is possible to make more accurate and reliable density measurements.

Here is an example of how to calculate the uncertainty in density measurements using the standard deviation method. Suppose we have a set of density measurements for a material. The measurements are:

1.23 g/cm^3
1.25 g/cm^3
1.22 g/cm^3

The mean of these measurements is 1.2333 g/cm^3. The standard deviation of the measurements is 0.0124 g/cm^3. Therefore, the uncertainty in the density measurement is 0.0124 g/cm^3. This means that we can be 95% confident that the true density of the material is within 0.0248 g/cm^3 of the mean measurement.