The Complete Order of Operations: A Mathematical Guide

_{November 3, 2023 by JoyAnswer.org, Category : Mathematics}

What is the complete order of operations? Understand the complete order of operations in mathematics, encompassing all the rules and guidelines for solving mathematical expressions.

Table of Contents

What is the complete order of operations?

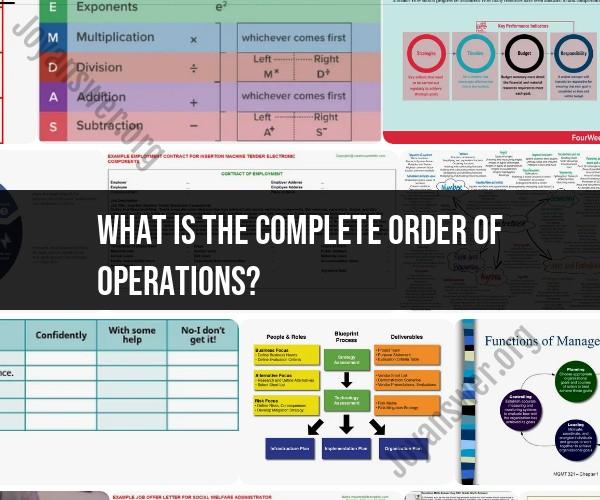
The complete order of operations, often remembered using the acronym PEMDAS, represents the sequence in which various mathematical operations should be performed in an expression to ensure accurate and consistent results. The order of operations is a fundamental concept in mathematics, particularly in algebra and arithmetic. Here is the complete order of operations:

P: Parentheses - Evaluate expressions inside parentheses first. This includes any nested or innermost parentheses.
E: Exponents - Calculate any values with exponents (powers and roots) next.
MD: Multiplication and Division - Perform multiplication and division from left to right as they appear in the expression. It's important to work from left to right in this step, as multiplication and division have the same level of precedence.
AS: Addition and Subtraction - Finally, perform addition and subtraction from left to right, as they appear in the expression. Like multiplication and division, addition and subtraction have the same level of precedence.

It's important to note that the order of operations ensures that mathematical expressions are evaluated consistently and correctly. Following these rules prevents ambiguity and ensures that the same expression is evaluated the same way by different individuals. It's a crucial concept for solving equations and simplifying expressions in mathematics.

Here's an example of how to use the complete order of operations:

Expression: 3 + 4 × (2^2 - 1)

Inside the parentheses: 2^2 - 1 = 4 - 1 = 3
Exponents: 3 + 4 × 3
Multiplication: 3 + 12
Addition: 15

So, the expression simplifies to 15 by following the complete order of operations (PEMDAS).

What is the complete sequence of the order of operations in mathematics?

The complete sequence of the order of operations in mathematics is as follows:

Parentheses

Exponents

Multiplication and division (from left to right)

Addition and subtraction (from left to right)

This sequence is often remembered by the acronyms PEMDAS or BODMAS.

Understanding the PEMDAS/BODMAS acronyms: How to remember the order of operations

PEMDAS and BODMAS are acronyms that stand for the following:

PEMDAS: Parentheses, Exponents, Multiplication and Division, Addition and Subtraction
BODMAS: Brackets, Orders, Division and Multiplication, Addition and Subtraction

Both acronyms refer to the same order of operations, and they can be used interchangeably.

Here is a mnemonic device that you can use to remember the order of operations:

Please Excuse My Dear Aunt Sally.

The first letter of each word in the mnemonic corresponds to a step in the order of operations:

Parentheses
Exponents
Multiplication
Division
Addition
Subtraction

How to apply the order of operations to solve math problems with multiple operations

To solve math problems with multiple operations, you should apply the order of operations as follows:

Evaluate any expressions within parentheses.
Evaluate any exponents.
Perform any multiplication and division operations from left to right.
Perform any addition and subtraction operations from left to right.

Here is an example of how to apply the order of operations to solve a math problem:

5 + (2 * 3) - 1

First, we evaluate the expression within the parentheses:

5 + (6) - 1

Next, we add the numbers in the parentheses to the first number:

5 + 6 - 1

Finally, we subtract the last number from the sum:

5 + 6 - 1 = 10

Exploring the significance of maintaining order in mathematical calculations

Maintaining order in mathematical calculations is significant because it ensures that the calculations are performed correctly. If the order of operations is not followed, the answer to the problem may be incorrect.

For example, consider the following problem:

5 + 2 * 3

If we do not follow the order of operations, we might multiply 2 and 3 first, and then add 5. This would give us an answer of 11. However, if we follow the order of operations correctly, we would add 5 and 2 first, and then multiply the sum by 3. This would give us an answer of 21.

Therefore, it is important to maintain order in mathematical calculations to ensure that the calculations are performed correctly.

Advanced order of operations: Handling nested parentheses and brackets

Nested parentheses and brackets occur when there is one or more expressions within a pair of parentheses or brackets. To handle nested parentheses and brackets, you should simply apply the order of operations from the inside out.

For example, consider the following problem: