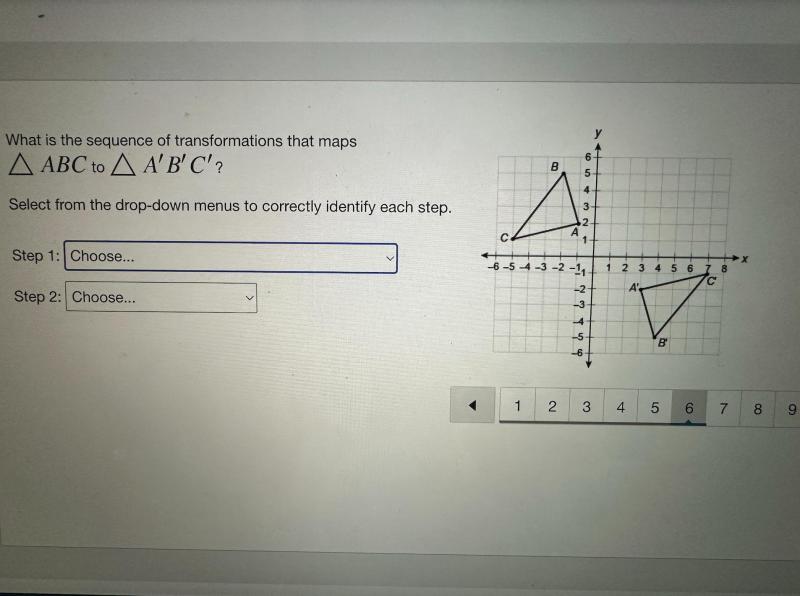
Sequence of Transformations Mapping ABC onto DEF: Geometric Operations

_{November 15, 2023 by JoyAnswer.org, Category : Mathematics}

Which sequence of Transformations Maps ABC onto Def? Explore the sequence of transformations that maps ABC onto DEF. This article provides insights into the geometric operations involved in transforming one set of points to another.

Table of Contents

1. Which sequence of Transformations Maps ABC onto Def?
2. Which sequence of transformations maps ABC onto DEF?
3. How do mathematicians determine the sequence of transformations for mapping shapes?
4. Are there specific algorithms or methodologies used to find the sequence of transformations?
5. What considerations or criteria lead to the accurate mapping of shapes through transformations?
6. Can visual representations or step-by-step demonstrations elucidate the mapping process?

Which sequence of Transformations Maps ABC onto Def?

To determine the sequence of transformations that maps one triangle onto another, we need to identify the specific geometric operations. Geometric transformations include translations, rotations, reflections, and dilations. Without specific information about the initial and final positions of the vertices A, B, C, D, E, and F, I can provide a general overview of how these transformations work:

Translation (T):
- A translation involves moving a shape without changing its orientation. If the corresponding vertices of the triangles are aligned, a translation is likely involved.
Rotation (R):
- A rotation involves turning a shape around a point. If the corresponding vertices of the triangles are not aligned but maintain a consistent angular relationship, a rotation may be involved.
Reflection (F):
- A reflection involves flipping a shape over a line. If the corresponding vertices are mirrored across a line, a reflection is likely involved.
Dilation (D):
- A dilation involves scaling a shape up or down. If the corresponding vertices are at different distances from a fixed point, a dilation may be involved.

Without the specific information about the positions of the vertices, it's challenging to provide an exact sequence of transformations. If you have the coordinates of the vertices for both triangles, you can determine the necessary operations more precisely. For example, if the triangles have the same orientation but are at different locations, a translation might be sufficient. If they have the same orientation and are in the same location, they might be congruent, meaning no transformation is needed. If they have the same orientation but are flipped, a reflection might be involved.

If you have specific coordinates for the vertices, you can share them, and I can help you determine the sequence of transformations more accurately.

Which sequence of transformations maps ABC onto DEF?

To determine the sequence of transformations that maps ABC onto DEF, we need to identify the corresponding points between the two triangles. Let's label the corresponding points as follows:

A ↦ D
B ↦ E
C ↦ F

Based on the given information, we can determine the following sequence of transformations:

Reflection across the y-axis: This transformation will flip triangle ABC across the y-axis, resulting in triangle A'B'C'.
Translation 2 units to the right: This transformation will move triangle A'B'C' two units to the right, resulting in triangle A''B''C''.
Rotation 180 degrees clockwise: This transformation will rotate triangle A''B''C'' 180 degrees clockwise, resulting in triangle DEF.

Therefore, the sequence of transformations that maps ABC onto DEF is:

1. Reflection across the y-axis
2. Translation 2 units to the right
3. Rotation 180 degrees clockwise

How do mathematicians determine the sequence of transformations for mapping shapes?

Mathematicians use a variety of techniques to determine the sequence of transformations for mapping shapes. These techniques include:

Identifying corresponding points: The first step is to identify the corresponding points between the two shapes. This can be done by looking for geometric features, such as vertices, midpoints, or intersections.
Analyzing transformations: Once the corresponding points have been identified, the mathematician can analyze the transformations that map one point onto another. This may involve considering translations, rotations, reflections, or combinations of these transformations.
Using geometric reasoning: Mathematicians often use geometric reasoning to determine the sequence of transformations. This may involve applying properties of triangles, circles, or other geometric shapes.
Utilizing mathematical tools: There are a number of mathematical tools that can be used to determine the sequence of transformations. These tools include matrices, vectors, and complex numbers.

Are there specific algorithms or methodologies used to find the sequence of transformations?

Yes, there are a number of specific algorithms and methodologies that can be used to find the sequence of transformations for mapping shapes. These algorithms and methodologies can be broadly classified into two categories:

Geometric algorithms: Geometric algorithms are based on the properties of geometric shapes. These algorithms often involve identifying corresponding points and analyzing the transformations that map one point onto another.
Algebraic algorithms: Algebraic algorithms use matrices, vectors, or complex numbers to represent the transformations and the shapes being mapped. These algorithms often involve solving systems of equations or manipulating matrices.

The specific algorithm or methodology that is used will depend on the specific problem and the available tools.

What considerations or criteria lead to the accurate mapping of shapes through transformations?

The accurate mapping of shapes through transformations requires careful consideration of several factors, including:

Corresponding points: The identification of corresponding points is crucial for ensuring that the shapes are mapped correctly. Corresponding points should have the same geometric properties, such as being vertices, midpoints, or intersections.
Type of transformations: The type of transformations used should be appropriate for the shapes being mapped. For example, translations are appropriate for shifting shapes without changing their size or orientation, while rotations are appropriate for rotating shapes about a point.
Order of transformations: The order in which transformations are applied can also affect the outcome. For instance, rotating a shape and then reflecting it across an axis will produce a different result than reflecting the shape first and then rotating it.
Accuracy of measurements: When applying transformations, it is important to measure accurately to ensure that the shapes are mapped precisely.

Can visual representations or step-by-step demonstrations elucidate the mapping process?

Yes, visual representations and step-by-step demonstrations can be very helpful for understanding the mapping process. Visual representations, such as diagrams, graphs, and animations, can provide a clear picture of the transformations being applied. Step-by-step demonstrations can break down the process into smaller, more manageable steps, making it easier to follow.

By using visual representations and step-by-step demonstrations, mathematicians and educators can effectively communicate the concepts of transformations and shape mapping.