How can you tell what numbers are irrational?
An irrational number is a real number that cannot be expressed as a fraction of two integers and has a non-repeating, non-terminating decimal expansion. Here are several methods to identify irrational numbers:
Square Roots of Non-Perfect Squares:
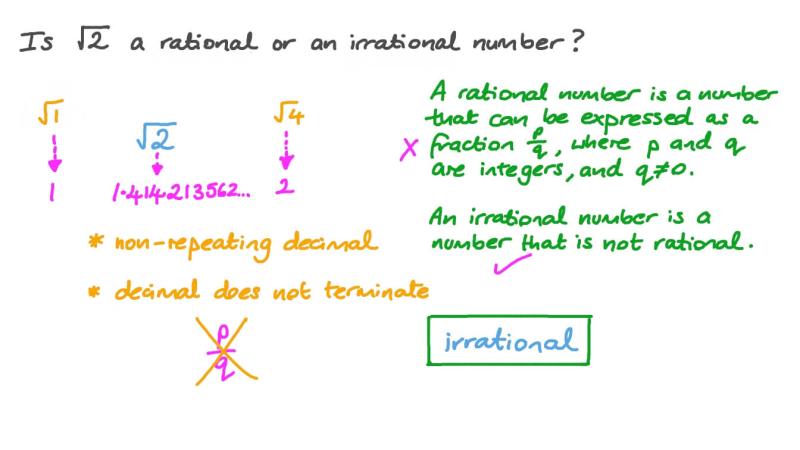
- The square root of any non-perfect square (a number whose square root is not an integer) is irrational. For example, the square root of 2, the square root of 3, and the square root of 5 are all irrational.
Non-Repeating, Non-Terminating Decimals:
- Numbers with decimal expansions that neither terminate (end) nor repeat are irrational. For example, the decimal representation of π (pi) is a non-repeating, non-terminating decimal.
Proofs by Contradiction:
- Some irrational numbers can be proven to be irrational through mathematical proofs by contradiction. For instance, the square root of 2 is proven to be irrational using a proof by contradiction known as the Pythagorean theorem.
Continued Fractions:
- Some irrational numbers have unique patterns in their continued fraction representations. If a number has a non-repeating pattern in its continued fraction expansion, it is likely irrational.
Algebraic Considerations:
- If a number is a root of a non-zero polynomial equation with integer coefficients, and the degree of the polynomial is higher than 1, then the number is irrational. For example, the roots of the equation are ±√2, both of which are irrational.
Euler's Identity:
- Euler's identity, which involves the mathematical constants , (the imaginary unit), and π, is an example of an equation where three transcendental numbers (numbers that are not algebraic) are combined in a non-trivial way: .
Transcendental Numbers:
- Transcendental numbers are a subset of irrational numbers that are not roots of any non-zero polynomial equation with integer coefficients. Examples include and π.
Proofs Using Number Theory:
- Certain irrational numbers can be identified through number theory, such as the irrationality of certain constants like Euler's constant or the Champernowne constant.
It's important to note that not all irrational numbers can be easily identified using simple rules, and some irrational numbers are known only through advanced mathematical proofs. However, the above methods cover many common examples of irrational numbers.
There are a number of ways to discern which numbers are irrational in mathematics. One common method is to use the definition of an irrational number. An irrational number is a number that cannot be expressed as a fraction of two integers. Another method for identifying irrational numbers is to use the fact that irrational numbers have non-repeating, non-terminating decimal expansions. This means that the decimal digits of an irrational number never repeat or end. Here are some examples of irrational numbers: All of these numbers have non-repeating, non-terminating decimal expansions.What methods or techniques are employed to identify and differentiate irrational numbers?
There are a number of mathematical methods and techniques that can be used to identify and differentiate irrational numbers. Some of these methods include:
- Proof by contradiction: This method involves assuming that a number is rational and then showing that this assumption leads to a contradiction. For example, the proof by contradiction that √2 is irrational shows that if √2 were rational, then it would have to be even, but this is impossible because the square of an even number is always even.
- Infinite series: Infinite series can be used to prove that certain numbers are irrational. For example, the infinite series expansion of π can be used to prove that π is irrational.
- Continued fractions: Continued fractions can be used to approximate irrational numbers. For example, the continued fraction expansion of π can be used to approximate π to any desired degree of accuracy.
Are there visual representations or patterns associated with irrational numbers?
There are some visual representations and patterns that are associated with irrational numbers. For example, the geometric representation of π is a circle. The circumference of a circle is equal to π times the diameter of the circle.
Another visual representation of irrational numbers is the Mandelbrot set. The Mandelbrot set is a fractal that contains an infinite number of irrational numbers.
However, it is important to note that not all irrational numbers have visual representations or patterns. For example, the number √2 does not have a known visual representation.