Formula for the Magnitude of a Vector: Mathematical Insights

_{October 2, 2023 by JoyAnswer.org, Category : Mathematics}

What is the formula for the magnitude of a vector? Explore the mathematical formula used to calculate the magnitude (length) of a vector in vector mathematics.

Table of Contents

What is the formula for the magnitude of a vector?

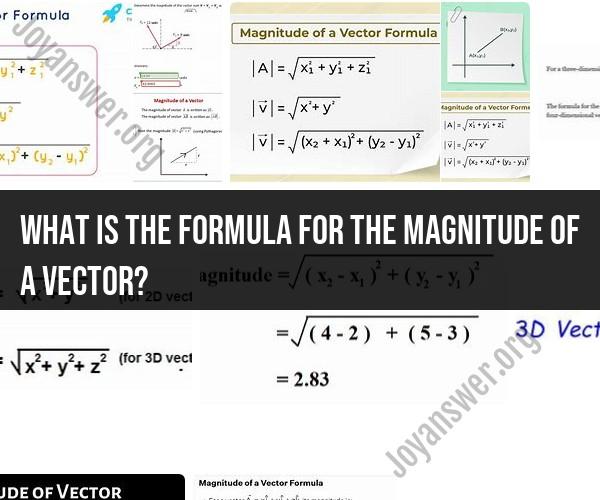
The formula for the magnitude (or length) of a vector in a two-dimensional or three-dimensional space is derived from the Pythagorean theorem. The magnitude of a vector "V," represented as ||V|| (double bars around "V"), is calculated as follows:

For a 2D vector (in the x-y plane):If V = (Vx, Vy), where Vx is the component of the vector along the x-axis, and Vy is the component along the y-axis, then the magnitude is given by:

||V|| = √(Vx² + Vy²)

For a 3D vector (in 3D space):If V = (Vx, Vy, Vz), where Vx is the x-component, Vy is the y-component, and Vz is the z-component, then the magnitude is calculated as:

||V|| = √(Vx² + Vy² + Vz²)

In both cases, you square each component, sum the squares, and then take the square root of the sum to find the magnitude of the vector. This is essentially the application of the Pythagorean theorem in multiple dimensions.

For example, consider a 2D vector V = (3, 4). To find its magnitude:

||V|| = √(3² + 4²) = √(9 + 16) = √25 = 5

So, the magnitude of the vector V = (3, 4) is 5 units.

This formula can be extended to vectors in higher-dimensional spaces by adding the squares of the components along each dimension and taking the square root of the sum. The magnitude of a vector represents its length or size and is a fundamental concept in vector mathematics, frequently used in physics, engineering, and other fields to describe physical quantities like velocity, force, displacement, and more.

Vector Magnitude Formula: Calculating the Size of Vectors

The vector magnitude formula is used to calculate the size of a vector. The magnitude of a vector is also known as its length.

The vector magnitude formula in two dimensions is:

|v| = √(vx^2 + vy^2)

where:

|v| is the magnitude of the vector
vx is the x-component of the vector
vy is the y-component of the vector

The vector magnitude formula in three dimensions is:

|v| = √(vx^2 + vy^2 + vz^2)

where:

vz is the z-component of the vector

Mathematics of Vectors: The Formula for Vector Magnitude

The vector magnitude formula is derived from the Pythagorean theorem. The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

The vector magnitude formula can be thought of as a generalization of the Pythagorean theorem to higher dimensions. In two dimensions, the vector magnitude formula is equivalent to the Pythagorean theorem. In three dimensions, the vector magnitude formula is equivalent to the Pythagorean theorem applied to the three components of the vector.

Measuring Direction and Magnitude: Using the Vector Magnitude Formula

The vector magnitude formula can be used to measure both the direction and magnitude of a vector.

To measure the direction of a vector, we can use the following formula:

θ = tan^-1(vy / vx)

where:

θ is the angle that the vector makes with the positive x-axis

To measure the magnitude of a vector, we can use the vector magnitude formula.

For example, consider the vector v = (2, 3). The magnitude of this vector is:

|v| = √(2^2 + 3^2) = √13

The direction of this vector is:

θ = tan^-1(3 / 2) = 56.31 degrees

Therefore, the vector v has a magnitude of √13 and a direction of 56.31 degrees.

The vector magnitude formula is a powerful tool for understanding and working with vectors. By understanding the vector magnitude formula, we can better understand the world around us.