Calculating Inverse Functions: Mathematical Procedures

_{October 13, 2023 by JoyAnswer.org, Category : Mathematics}

How to calculate inverse functions? Understand the mathematical procedures for calculating inverse functions, an essential concept in mathematics.

Table of Contents

How to calculate inverse functions?

Calculating the inverse of a function involves finding a new function that undoes the work of the original function. In other words, if you have a function $f(x)$ , the inverse function $f^{-1}(x)$ is such that $f(f^{-1}(x)) = x$ for all values of $x$ . Here are the general steps to calculate the inverse of a function:

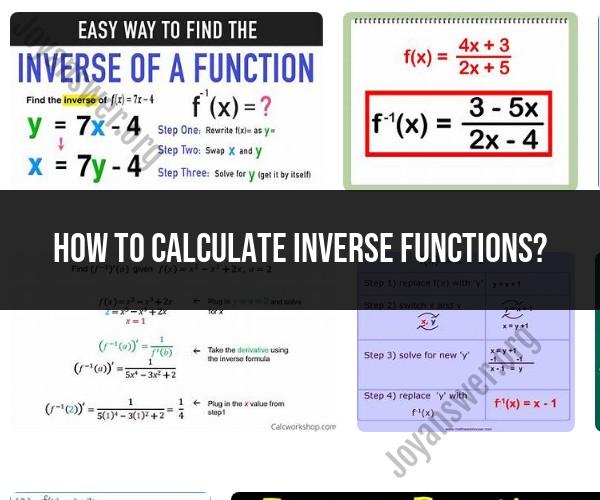
1. Start with the original function: Let's say you have a function $f(x)$ .

2. Replace $f(x)$ with $y$ : This step is often used to make the process more intuitive. Replace $f(x)$ with $y$ so that you have the equation $y = f(x)$ .

3. Swap $x$ and $y$ : Interchange $x$ and $y$ , so the equation becomes $x = f(y)$ .

4. Solve for $y$ : Rearrange the equation to solve for $y$ , which will be the inverse function $f^{-1}(x)$ . This means that you need to isolate $y$ on one side of the equation. The result should be in the form $y = f^{-1}(x)$ .

5. Replace $y$ with $f^{-1}(x)$ : After solving for $y$ , replace $y$ with $f^{-1}(x$ in the equation to express the inverse function as $f^{-1}(x) = \text{some expression in terms of } x$ .

6. Verify the domain: Check the domain of the original function, as it can impact the domain of the inverse function. In some cases, you may need to restrict the domain of the original function to ensure the inverse is a function.

7. Test the inverse: To verify that you've calculated the correct inverse function, make sure that $f(f^{-1}(x)) = x$ and $f^{-1}(f(x)) = x$ for all values of $x$ . This shows that the inverse function undoes the work of the original function.

It's important to note that not all functions have inverses. For a function to have an inverse, it must pass the horizontal line test, meaning that no horizontal line intersects the graph of the function more than once. Additionally, some functions have restricted domains that need to be considered when finding their inverses. For example, square root functions are typically restricted to non-negative values.

The process of finding inverse functions can be straightforward for simple functions, but it can become more complex for more intricate functions. In such cases, algebraic manipulation and solving for $y$ may involve more advanced techniques. However, the general approach outlined above remains the same.

Understanding Inverse Functions in Mathematics

An inverse function is a function that reverses the operation of another function. In other words, if f(x) = y, then the inverse function of f, denoted by f−1(x), is the function that satisfies f−1(y) = x.

Not all functions have inverse functions. For example, the function f(x) = x^2 does not have an inverse function because it fails the horizontal line test. The horizontal line test states that a function has an inverse function if and only if each horizontal line intersects the function's graph at most once.

Methods for Calculating Inverse Functions

There are two main methods for calculating inverse functions:

Analytical method: This method involves solving the equation f(x) = y for x. Once x is solved for in terms of y, the inverse function is simply f−1(y) = x.
Graphical method: This method involves reflecting the graph of f(x) across the line y = x. The reflected graph is the graph of the inverse function, f−1(x).

Practical Applications of Inverse Functions

Inverse functions have many practical applications in mathematics, science, and engineering. Some examples include:

Cryptography: Inverse functions are used in cryptography to encrypt and decrypt messages.
Physics: Inverse functions are used in physics to calculate the inverse of various physical quantities, such as velocity and acceleration.
Engineering: Inverse functions are used in engineering to design and analyze systems and devices.

Common Mistakes and Challenges in Calculating Inverse Functions

A common mistake in calculating inverse functions is to assume that all functions have inverse functions. As mentioned above, not all functions have inverse functions.

Another common mistake is to not restrict the domain of the inverse function. If the original function is not defined for all real numbers, then the inverse function will also not be defined for all real numbers.

Examples of Finding Inverse Functions for Different Types of Functions

Here are some examples of finding inverse functions for different types of functions:

Linear function: The inverse of a linear function is another linear function. For example, the inverse of the function f(x) = mx + b is the function f−1(x) = (x - b)/m.
Quadratic function: The inverse of a quadratic function is not a quadratic function. For example, the inverse of the function f(x) = x^2 is the function f−1(x) = ±√x.
Exponential function: The inverse of an exponential function is a logarithmic function. For example, the inverse of the function f(x) = ax^b is the function f−1(x) = log_a(x).
Logarithmic function: The inverse of a logarithmic function is an exponential function. For example, the inverse of the function f(x) = log_a(x) is the function f−1(x) = a^x.

Conclusion

Inverse functions are a powerful tool in mathematics and have many practical applications. By understanding the concept of inverse functions and how to calculate them, you can expand your problem-solving abilities and solve a wider range of problems.