Using Sin, Cos, and Tan in Trigonometry: Practical Guide

_{November 7, 2023 by JoyAnswer.org, Category : Mathematics}

How do you use Sin Tan Cos? Discover how to use sin, cos, and tan in trigonometry to solve problems involving angles, triangles, and other mathematical scenarios.

Table of Contents

How do you use Sin Tan Cos?

Sine (sin), cosine (cos), and tangent (tan) are trigonometric functions used in trigonometry to relate the angles and side lengths of a right triangle. These functions are fundamental in solving various problems in geometry, physics, engineering, and more. Here's a practical guide on how to use these trigonometric functions:

Understanding Trigonometric Functions:
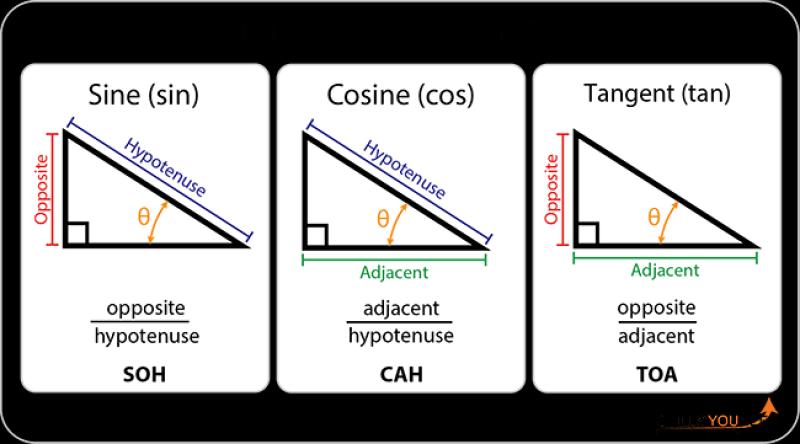
- Sine (sin): The sine of an angle in a right triangle is the ratio of the length of the side opposite that angle to the length of the hypotenuse. In a right triangle with an angle θ, sin(θ) = (opposite side length) / (hypotenuse length).
- Cosine (cos): The cosine of an angle is the ratio of the length of the side adjacent to that angle to the length of the hypotenuse. In the same right triangle, cos(θ) = (adjacent side length) / (hypotenuse length).
- Tangent (tan): The tangent of an angle is the ratio of the sine of the angle to the cosine of the angle. In mathematical terms, tan(θ) = sin(θ) / cos(θ).
Useful Trigonometric Relationships:
- Pythagorean Identity: In a right triangle, the Pythagorean theorem states that the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. This can be expressed as: $a^2 + b^2 = c^2$ , where $c$ is the hypotenuse, and $a$ and $b$ are the other two sides.
- Reciprocal Identities: The reciprocal identities are related to the main trigonometric functions:
  - $\csc(θ) = 1/\sin(θ)$
  - $\sec(θ) = 1/\cos(θ)$
  - $\cot(θ) = 1/\tan(θ)$
Solving Right Triangle Problems:
- Trigonometric functions are commonly used to solve right triangle problems. Given an angle and one side length, you can use sine, cosine, or tangent to find other side lengths or angles.
- Identify the angle of interest, the side lengths, and the trigonometric function to use based on the given information.
- Use the appropriate trigonometric function to set up an equation and solve for the unknown value.
Common Applications:
- Trigonometry is used in various practical applications, such as:
  - Calculating distances and heights (e.g., measuring the height of a tree or the distance to a faraway object).
  - Analyzing angles in geometry, navigation, and surveying.
  - Modeling periodic phenomena (e.g., sound waves, light waves, and oscillations) in physics.
  - Solving problems related to right triangles in engineering and construction.
Trigonometric Tables and Calculators:
- Trigonometric tables provide precomputed values of trigonometric functions for specific angles. They were historically used before calculators became common.
- Calculators and computer software make it easier to calculate trigonometric values, allowing you to work with angles and side lengths more efficiently.

Remember to use the correct trigonometric function and the appropriate units (degrees or radians) when working with trigonometric problems. Understanding these functions is essential for solving a wide range of mathematical and practical problems involving triangles and angles.

1. Utilizing Sine, Cosine, and Tangent: A Guide to Trigonometry

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. The three primary trigonometric functions, sine (sin), cosine (cos), and tangent (tan), are used to express these relationships.

Sine (sin):

Sine is defined as the ratio of the opposite side to the hypotenuse in a right triangle. It is represented by the abbreviation "sin" and can be calculated using the following formula:

sin θ = opposite / hypotenuse

Cosine (cos):

Cosine is defined as the ratio of the adjacent side to the hypotenuse in a right triangle. It is represented by the abbreviation "cos" and can be calculated using the following formula:

cos θ = adjacent / hypotenuse

Tangent (tan):

Tangent is defined as the ratio of the opposite side to the adjacent side in a right triangle. It is represented by the abbreviation "tan" and can be calculated using the following formula:

tan θ = opposite / adjacent

Trigonometric Functions: How to Apply Sin, Cos, and Tan

Trigonometric functions have a wide range of applications in various fields, including:

Navigation: Trigonometric functions are used to calculate distances, angles, and directions in navigation systems.
Surveying: Trigonometric functions are used to measure distances and angles in surveying and mapping.
Engineering: Trigonometric functions are used in various engineering calculations, such as designing structures, calculating forces, and analyzing motion.
Physics: Trigonometric functions are used in physics to model waves, analyze motion, and study the properties of light.
Graphics: Trigonometric functions are used in computer graphics to create realistic images, animations, and special effects.

Trigonometry Essentials: Using Sin, Cos, and Tan in Calculations

Here are some examples of how to use sine, cosine, and tangent in calculations:

Finding a missing side of a triangle: Given one side and an angle of a right triangle, you can use sine, cosine, or tangent to find the missing side.
Solving for an unknown angle: Given two sides of a right triangle, you can use inverse trigonometric functions (arcsin, arccos, arctan) to solve for the unknown angle.
Converting between degrees and radians: Trigonometric functions can be used to convert between angles measured in degrees and angles measured in radians.
Modeling periodic phenomena: Sine and cosine functions can be used to model periodic phenomena, such as waves, oscillations, and fluctuations.

Trigonometry is a fundamental tool in mathematics, science, and engineering. Understanding sine, cosine, and tangent is essential for solving a wide range of problems in these fields.