Unveiling Vertical Shifts in Trigonometric Functions

_{December 8, 2023 by JoyAnswer.org, Category : Mathematics}

How to find the vertical shift of a trig function? Explore techniques to identify and calculate the vertical shift in trigonometric functions. Understand how this shift impacts the function's position.

How to find the vertical shift of a trig function?

The vertical shift of a trigonometric function refers to the upward or downward displacement of the graph along the y-axis. This shift is determined by a constant added to the function, and it affects the position of the entire graph without altering its shape.

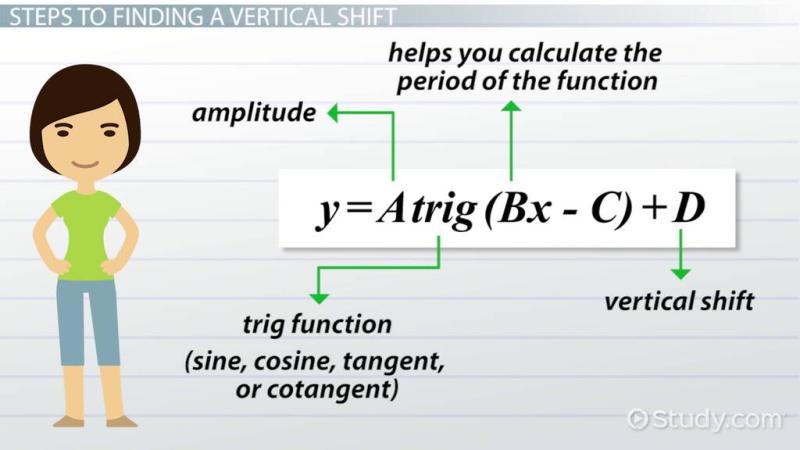
The general form of a trigonometric function with a vertical shift is:

$f(x) = A \cdot \sin(Bx + C) + D$

$f(x) = A \cdot \cos(Bx + C) + D$

where:

$A$ is the amplitude (the vertical distance from the midline to the maximum or minimum),
$B$ is the frequency (controls the period of the function),
$C$ is the phase shift (horizontal shift),
$D$ is the vertical shift.

To find the vertical shift ( $D$ ), you need to look at the constant term that is added to the function. If the original function is $f(x) = \sin(x)$ or $f(x) = \cos(x)$ , then the vertical shift is the constant term added to it.

For example: $f(x) = \sin(x) + 2$

In this case, the vertical shift ( $D$ ) is 2 units upward. If the constant term were -2, the shift would be 2 units downward.

Similarly, for a cosine function: $g(x) = \cos(x - \pi) - 3$

Here, the vertical shift ( $D$ ) is -3 units downward.

To summarize, identify the constant term in the trigonometric function, and the value of that constant will tell you the vertical shift and its direction (upward or downward).

Determining the Vertical Shift in Trigonometric Functions

The vertical shift of a trigonometric function is the amount it moves up or down from its standard position. There are several methods to determine this shift:

1. Analyzing the Equation:

The standard equation of a sine function is y = sin(x), and the standard equation of a cosine function is y = cos(x). Any constant added or subtracted to the function will cause a vertical shift.

Positive constant: Adding a positive constant shifts the function up by the value of the constant.

Negative constant: Subtracting a constant shifts the function down by the absolute value of the constant.

For example, the equation y = sin(x) + 2 represents a sine function that has been shifted two units upwards.

2. Graphing:

We can also determine the vertical shift by graphing the function and comparing it to the standard graph.

If the graph is above the standard graph, it has been shifted upwards. The vertical distance between the two graphs represents the amount of shift.

If the graph is below the standard graph, it has been shifted downwards. The vertical distance between the two graphs represents the amount of shift.

3. Amplitude and Midline:

The amplitude and midline of a trigonometric function can also provide information about the vertical shift.

Amplitude: The amplitude of a function is the absolute value of the coefficient multiplying the trigonometric term. It determines the vertical distance between the peaks and troughs of the graph.

Midline: The midline is the horizontal line that passes exactly in the middle of the function's range.

For example, the function y = 2 sin(x) + 1 has an amplitude of 2 and a midline of y = 1. This tells us that the function has been stretched vertically by a factor of 2 and shifted up by 1 unit.

How Coefficients Affect the Vertical Shift:

The vertical shift of a trigonometric function is primarily affected by the constant term added or subtracted to the function. This constant directly determines the amount and direction of the shift.

Coefficient of the trigonometric term: This coefficient affects the amplitude of the function, but not the vertical shift. Changing the coefficient will stretch or compress the graph vertically but will not move it up or down.

Phase shift: A phase shift moves the graph horizontally to the left or right. It does not affect the vertical position of the graph.

In summary, determining the vertical shift of a trigonometric function involves analyzing the equation, considering the amplitude and midline, and examining the constant term added or subtracted. By understanding the impact of different coefficients, we can interpret and analyze various trigonometric functions with greater ease.