How do you find the tangent line of a curve?
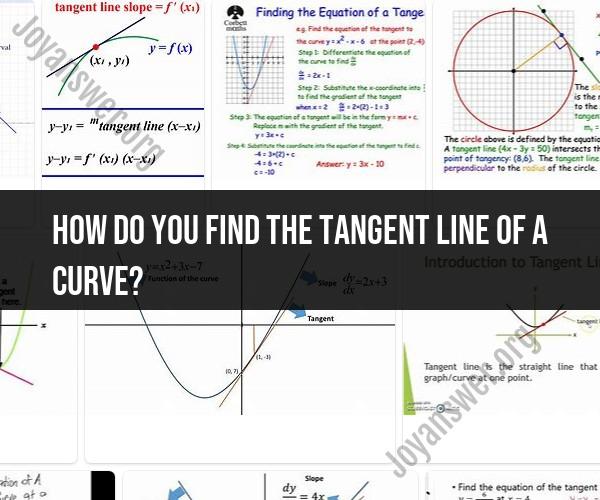
To find the tangent line of a curve at a specific point, you'll need to follow these steps:
Identify the Point of Tangency: Determine the point on the curve where you want to find the tangent line. You'll need the x-coordinate (let's call it "a") at this point.
Find the Derivative: Calculate the derivative of the function that defines the curve. The derivative represents the slope of the tangent line at any given point on the curve. Use the following notation: f'(x) or dy/dx.
Evaluate the Derivative: Plug the x-coordinate of the point of tangency (a) into the derivative function to find the slope of the tangent line at that specific point: f'(a).
Write the Equation of the Tangent Line: Now that you have the slope (m) of the tangent line at point (a), you can use the point-slope form of a linear equation to write the equation of the tangent line. The point-slope form is:
y - y₁ = m(x - x₁)
- (x₁, y₁) represents the point of tangency (a, f(a)).
- m represents the slope of the tangent line, which is f'(a).
Plug in the values to get the equation of the tangent line.
Simplify the Equation: If necessary, simplify the equation of the tangent line by solving for y.
That's it! You've now found the equation of the tangent line to the curve at the specific point of interest. This tangent line represents the best linear approximation of the curve near that point.
Keep in mind that finding the derivative and evaluating it at a specific point (step 3) is a key concept in calculus. The derivative gives you the slope of the tangent line at any point on the curve.