What does a negative plus a negative number equal?
When you add two negative numbers together, the result is another negative number. In arithmetic, the addition of negatives follows a specific rule:
Rule for Adding Negative Numbers:
If you have two negative numbers, when you add them, you sum their magnitudes (absolute values) and give the result the negative sign.
Mathematically, if you have -a + (-b), the result is - (a + b).
Here's an example:
- If you add
-3and-5, you first add their magnitudes (ignoring the signs):3 + 5 = 8. - Then, you assign the negative sign to the result:
-8.
So, -3 + (-5) = -8.
In summary, adding two negative numbers results in a negative number, and you simply add their magnitudes to find the magnitude of the result. The negative sign is then applied to the sum of magnitudes.
Navigating Arithmetic: The Outcome of Adding Negative Numbers
When adding negative numbers, it's crucial to remember that they represent values less than zero. Here's what happens when you combine them:
What happens when you add two negative numbers together?
- The result is always a negative number.
- The sum's absolute value (its distance from zero) is the combined absolute values of the original numbers.
For example:
- (-5) + (-3) = -8
- (-10) + (-2) = -12
Rules and Conventions in Adding Negative Numerals
- Adding a negative number is like moving to the left on the number line.- Adding two negative numbers means moving even further to the left, resulting in a larger negative number.
Key Rules:
- Adding Two Negative Numbers: Results in a negative number greater in magnitude than either original number.
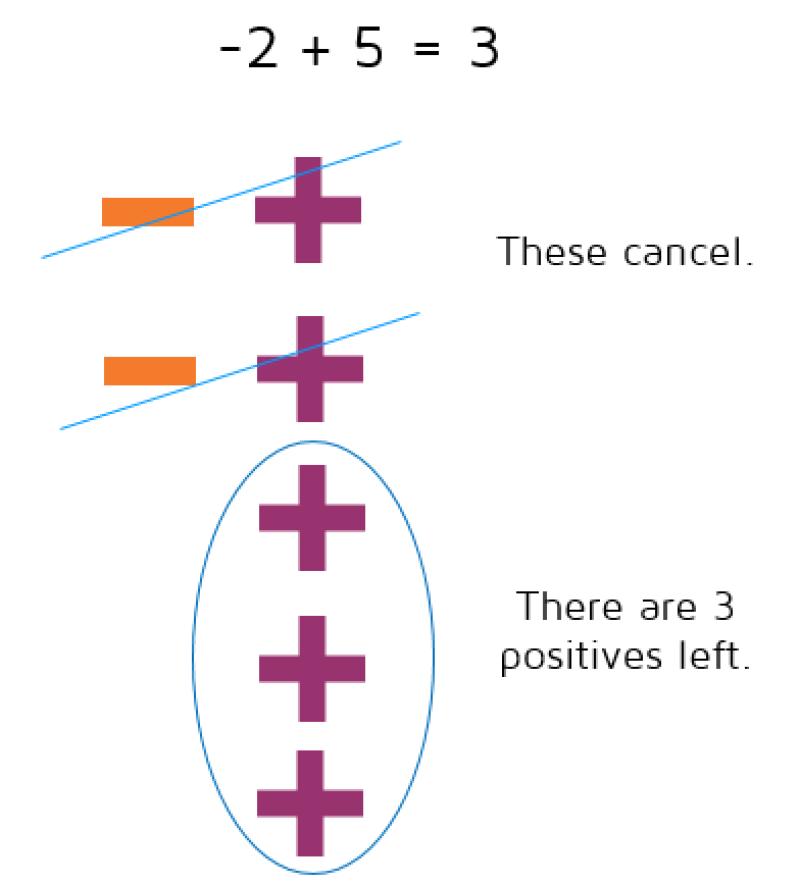
- Adding a Negative Number to a Positive Number:
- Sum is smaller than the positive number.
- Sign of the sum depends on the magnitudes of the numbers.
- Triangle Inequality: The absolute value of the sum is always less than or equal to the sum of the absolute values of the original numbers.
Example:
- 5 + (-3) = 2 (positive sum, as 5 is larger than 3)
- 2 + (-5) = -3 (negative sum, as 5 is larger than 2)
Visualizing on a Number Line:
- Imagine a number line with 0 in the center, positive numbers to the right, and negative numbers to the left.
- Adding a negative number is like moving to the left.
- Adding two negative numbers means taking two leftward steps, resulting in a position further to the left (a larger negative number).