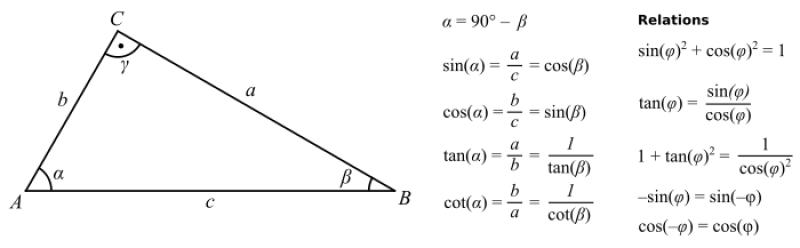
What is the sin cos tan formula?
The sine (sin), cosine (cos), and tangent (tan) functions are fundamental trigonometric functions used in mathematics to relate the angles and sides of a right triangle. These functions are defined based on the ratios of the sides of a right triangle. Here are the basic formulas for sin, cos, and tan:
Sine (sin):
- The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle (the "opposite side") to the length of the hypotenuse. Mathematically, it's represented as:
sin(θ) = (opposite side) / (hypotenuse)Cosine (cos):
- The cosine of an angle is defined as the ratio of the length of the side adjacent to the angle (the "adjacent side") to the length of the hypotenuse. Mathematically, it's represented as:
cos(θ) = (adjacent side) / (hypotenuse)Tangent (tan):
- The tangent of an angle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. Mathematically, it's represented as:
tan(θ) = (opposite side) / (adjacent side)
These trigonometric functions are used to relate the angles of a right triangle to the lengths of its sides. They are fundamental tools in trigonometry and have applications in various fields, including mathematics, physics, engineering, and more. The values of sin, cos, and tan depend on the measure of the angle (θ) and the lengths of the sides in the right triangle.
Understanding the Sin, Cos, and Tan Formulas
Sin (sine) represents the ratio of the opposite side to the hypotenuse in a right triangle.
Cos (cosine) represents the ratio of the adjacent side to the hypotenuse in a right triangle.
Tan (tangent) represents the ratio of the opposite side to the adjacent side in a right triangle.
These trigonometric functions are essential for understanding and solving problems involving angles and triangles.
Deriving and Using Trigonometric Formulas
Trigonometric formulas can be derived using the Pythagorean theorem and basic algebraic relationships. These formulas are used to solve a wide range of trigonometric problems, including:
Finding the missing side or angle in a right triangle
Analyzing periodic phenomena, such as waves and oscillations
Representing complex numbers and performing complex number operations
Modeling real-world phenomena, such as the motion of celestial bodies or the design of bridges and buildings
How to Solve Trigonometric Equations Using Sin, Cos, and Tan
Solving trigonometric equations involves using the inverse trigonometric functions (arcsin, arccos, arctan) to isolate the angle when given the trigonometric ratio. These functions can be found on most scientific calculators.
Here's a general approach to solving trigonometric equations:
Identify the trigonometric function: Determine which trigonometric function (sin, cos, or tan) is involved in the equation.
Isolate the trigonometric ratio: Manipulate the equation algebraically to isolate the trigonometric ratio on one side of the equation.
Apply the inverse trigonometric function: Use the appropriate inverse trigonometric function (arcsin, arccos, or arctan) to find the angle corresponding to the isolated trigonometric ratio.
Consider multiple solutions: Trigonometric functions may have multiple solutions within a given range. Check for additional solutions using the periodic nature of trigonometric functions.
Common Trigonometric Identities Involving Sin, Cos, and Tan
Trigonometric identities are equations that hold true for all angles. These identities are useful for simplifying trigonometric expressions and solving trigonometric problems.
Here are some common trigonometric identities:
Pythagorean identity: sin² θ + cos² θ = 1
Reciprocal identities: cosec θ = 1 / sin θ, sec θ = 1 / cos θ, cot θ = 1 / tan θ
Double-angle identities: sin 2θ = 2sin θ cos θ, cos 2θ = cos² θ - sin² θ, tan 2θ = 2tan θ / (1 - tan² θ)
Sum and difference identities: sin (θ + φ) = sin θ cos φ + cos θ sin φ, cos (θ + φ) = cos θ cos φ - sin θ sin φ, tan (θ + φ) = (tan θ + tan φ) / (1 - tan θ tan φ)
Trigonometric Formulas for Special Angles
Trigonometric formulas for special angles (0°, 30°, 45°, 60°, 90°) can be memorized or derived using the unit circle. These values are useful for solving trigonometric problems and understanding the behavior of trigonometric functions.
Here's a table of trigonometric values for special angles:
| Angle | Sin | Cos | Tan |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | √3/3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | undefined |