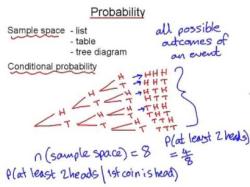
Probability of B Given A: Understanding Conditional Probability

The probability of event B occurring given that event A has already occurred is denoted as P(B|A), which is read as "the probability of B given A." Conditional probability is used to assess the likelihood of one event happening, taking into account the knowledge that another event has already occurred.

Mathematically, conditional probability is calculated using the following formula:

$P(B|A) = \frac{P(A \text{ and } B)}{P(A)}$

Where:

• P(B|A) is the conditional probability of B given A.
• P(A and B) is the probability of both events A and B happening.
• P(A) is the probability of event A happening.

To calculate P(B|A), you need to know both P(A and B) and P(A). If you have this information, you can use the formula to find the conditional probability.

Here's an example to illustrate:

Let's say we have a deck of playing cards, and we want to find the probability of drawing a red card (event A) given that we've already drawn a heart card (event B).

• P(A): Probability of drawing a red card = 26/52 (there are 26 red cards out of 52 cards in a deck).
• P(B): Probability of drawing a heart card = 13/52 (there are 13 heart cards out of 52).

Now, let's say we've drawn a heart card, so event B has occurred. To find P(A|B), we use the formula:

$P(A|B) = \frac{P(A \text{ and } B)}{P(B)}$

In this case, P(A and B) is the probability of drawing a red heart card, which is 1/52 (there is only one red heart card in the deck).

So, $P(A|B) = \frac{1/52}{13/52} = \frac{1}{13}$

Therefore, the probability of drawing a red card given that we've already drawn a heart card is 1/13.

Here are a couple of examples to illustrate conditional probability:

1. Example 1 - Tossing Two Coins:Suppose you have two fair coins. Let A be the event that the first coin lands heads up, and B be the event that the second coin lands heads up. If you already know that the first coin is heads (event A has occurred), then the probability that the second coin is also heads (event B|A) is 0.5, because there are two equally likely outcomes (heads or tails) for the second coin.

2. Example 2 - Health Screening:Consider a medical test for a disease. Let A be the event that the test result is positive, and B be the event that a person actually has the disease. To find the conditional probability P(B|A), you would need to know the test's sensitivity (the probability of a positive result when the person has the disease) and its specificity (the probability of a negative result when the person does not have the disease). Conditional probability in this context can help assess the accuracy of the test.

Conditional probability is a fundamental concept in probability theory and is used in various fields, including statistics, machine learning, and real-world decision-making scenarios where events are dependent on each other.