Elements within a Sample Space: Understanding Basics
December 7, 2023 by JoyAnswer.org, Category : Probability
What are the elements in a sample space? Explore the fundamental elements constituting a sample space. Understand the basics of sample space components in probability theory.
What are the elements in a sample space?
In probability theory, a sample space represents the set of all possible outcomes of a random experiment or an event. The elements within a sample space are the individual outcomes that can occur when an experiment is conducted. These elements are often denoted as sample points and collectively form the sample space.
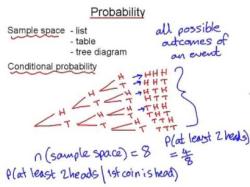
For instance, consider flipping a coin. The sample space for a single coin flip contains two possible outcomes: "heads" and "tails." Therefore, the elements or sample points within this sample space are "heads" and "tails."
In another example, rolling a six-sided die results in a sample space with six possible outcomes: {1, 2, 3, 4, 5, 6}. Each of these numbers represents a distinct sample point or element within the sample space of rolling a die.
It's important to note that the elements within a sample space encompass all the possible outcomes that can occur, and each outcome is mutually exclusive and collectively exhaustive. The sample space forms the basis for understanding probabilities associated with different events within the experiment or random process.
What constitutes the individual elements contained within a sample space?
The individual elements contained within a sample space are called outcomes. They represent all the possible results of an experiment or event. In other words, they are the exhaustive list of all possibilities that can occur.
Here are some key points about sample space elements:
- Mutually exclusive: Outcomes within a sample space are mutually exclusive, meaning that only one outcome can occur at a time.
- Collectively exhaustive: Together, the outcomes within a sample space account for all possible outcomes of the experiment or event.
- Specific: Each outcome should be clearly defined and unambiguous.
- Finite or infinite: A sample space can be finite (a limited number of possible outcomes) or infinite (an unlimited number of possible outcomes).
For example, if you toss a fair coin, the sample space would consist of two elements: heads and tails. These outcomes are mutually exclusive because the coin cannot land on both heads and tails at the same time. They are also collectively exhaustive because they account for all possible outcomes of the event.
Here are some additional examples of sample spaces and their elements:
- Rolling a die: Sample space = {1, 2, 3, 4, 5, 6}
- Drawing a card from a deck: Sample space = {52 different cards}
- Measuring the height of a student: Sample space = {all possible heights in cm}
Understanding the concept of sample space and its elements is fundamental to various branches of mathematics, including probability, statistics, and decision theory.
