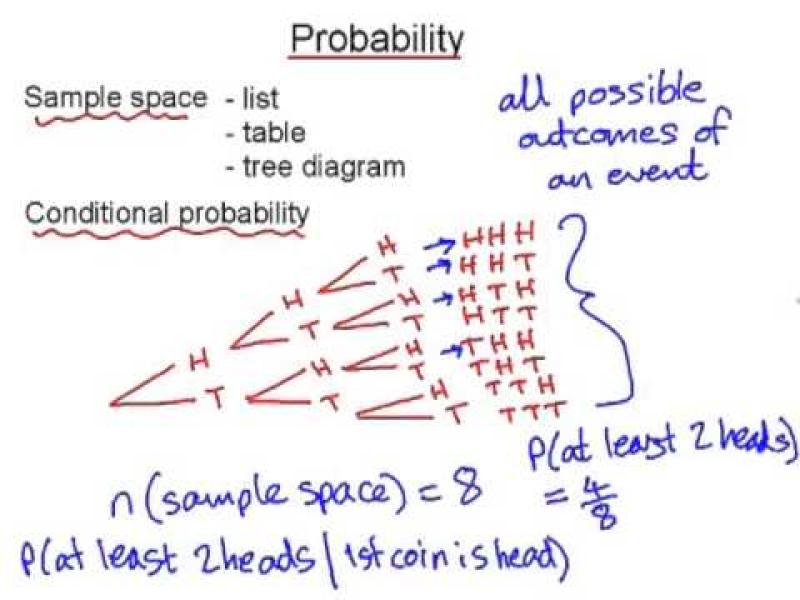
What is the probability of sample space?
The probability of an event within a sample space is calculated by dividing the number of favorable outcomes (those that satisfy the condition of the event) by the total number of possible outcomes in the sample space.
The formula for probability (P) of an event A within a sample space S is:
For instance, if you're rolling a fair six-sided die, the sample space S consists of six possible outcomes: {1, 2, 3, 4, 5, 6}.
Let's say you want to find the probability of rolling an even number (event A). The favorable outcomes for this event within the sample space are {2, 4, 6} (three even numbers).
Using the formula:
Therefore, the probability of rolling an even number on a fair six-sided die is or 50%.
In a sample space, the sum of probabilities of all possible events should equal 1 (or 100%). This principle is known as the law of total probability, ensuring that all possible outcomes cover the entire sample space.
How is the probability of a sample space defined or calculated in statistics?
In statistics, the probability of a sample space is always 1, regardless of the specific elements contained within it. This is because a sample space represents all possible outcomes of an event or experiment. By definition, if all possible outcomes are considered, there is a certainty that one of them will occur, making the probability 1.
Here's why the probability of a sample space is always 1:
- Mutually exclusive outcomes: The individual elements within a sample space are mutually exclusive. This means that only one outcome can occur at a time.
- Collectively exhaustive outcomes: Together, the elements within a sample space account for all possible outcomes. This means there are no other possibilities besides those included in the sample space.
Therefore, since all possible outcomes are included and only one can occur, the probability of the sample space must be 1.
Here's an example:
If you flip a fair coin, the sample space is {heads, tails}. There is a 100% chance that one of these outcomes will occur when you flip the coin, making the probability of the sample space 1.
The concept of sample space and its probability is fundamental to various branches of mathematics, including probability, statistics, and decision theory. Understanding this concept helps us interpret and analyze various situations involving chance and uncertainty.