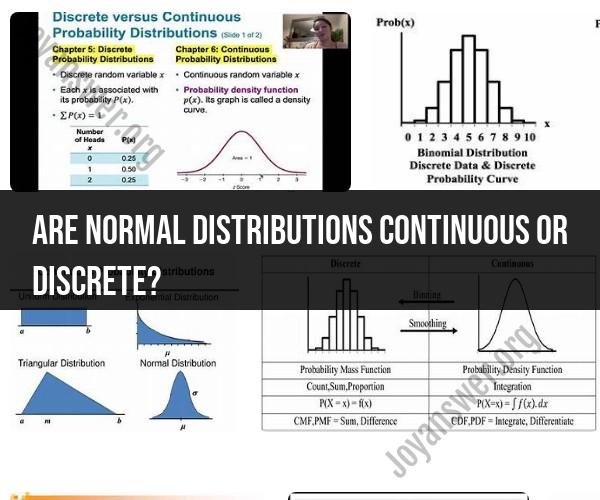
Normal Distributions: Continuous or Discrete?

_{October 21, 2023 by JoyAnswer.org, Category : Mathematics}

Are normal distributions continuous or discrete? Understand whether normal distributions are continuous or discrete probability distributions and the characteristics that define them.

Table of Contents

Are normal distributions continuous or discrete?

Normal distributions are continuous probability distributions. A continuous distribution is one where the random variable can take on an infinite number of possible values within a given range, and it is described by a continuous probability density function (PDF).

In the case of the normal distribution, also known as the Gaussian distribution, it is characterized by a bell-shaped curve, and it is completely continuous. This means that any real number within the range of the distribution is a possible value. The probability of a specific value occurring is technically zero because there are infinitely many possible values, and the distribution is defined over a continuous range.

The continuous nature of the normal distribution makes it suitable for modeling a wide range of real-world phenomena, including measurements such as height, weight, test scores, and many other natural and social processes. In contrast, discrete distributions, such as the Poisson distribution or the binomial distribution, describe random variables with a countable number of possible values and are used for scenarios where the outcome is counted in whole numbers or integers.

Normal Distributions: Bridging the Gap Between Continuous and Discrete

Normal distributions, also known as Gaussian distributions, are a type of continuous probability distribution that is symmetrical around its mean and has a bell-shaped curve. Normal distributions are found in many areas of science and engineering, including physics, chemistry, biology, and economics.

Discrete probability distributions, on the other hand, are probability distributions that only take on a finite number of values. For example, the number of heads obtained in flipping a coin three times is a discrete probability distribution.

Normal distributions can be thought of as a bridge between continuous and discrete probability distributions. In many cases, we can approximate a discrete probability distribution with a normal distribution. For example, the number of heads obtained in flipping a coin 100 times is approximately normally distributed.

The Mathematical Elegance of Normal Distributions

Normal distributions have a number of elegant mathematical properties. For example, the sum of two normally distributed variables is also normally distributed. This property is known as the central limit theorem.

Normal distributions are also closed under convolution. Convolutions are a type of mathematical operation that is used to combine probability distributions. The convolution of two normally distributed variables is also normally distributed.

Probability Distributions in Continuous and Discrete Worlds

Probability distributions are a way of representing the likelihood of different outcomes in a random experiment. In the continuous world, probability distributions are used to represent the likelihood of different values for continuous variables, such as height, weight, and temperature.

In the discrete world, probability distributions are used to represent the likelihood of different outcomes for discrete variables, such as the number of heads obtained in flipping a coin or the number of customers who visit a store in a day.

Real-World Applications and Interpretations of Normal Distributions

Normal distributions have many real-world applications. For example, normal distributions can be used to:

Predict the number of people who will attend a concert or sporting event.
Determine the quality control standards for a manufacturing process.
Design clinical trials for new drugs and medical treatments.
Analyze the results of standardized tests.

Normal distributions can also be used to interpret data from a variety of sources, such as:

The heights and weights of students in a school.
The scores on a standardized test.
The number of defective products produced by a manufacturing process.
The amount of rainfall in a particular region.

Unveiling the Beauty of Statistical Curves: A Normal Distribution Overview

Normal distributions are one of the most important and widely used statistical distributions in the world. They are found in many areas of science and engineering, and they have many real-world applications.

The bell-shaped curve of the normal distribution is a beautiful and elegant sight to behold. It is a reminder of the order and symmetry that exists in the natural world.

Normal distributions are also a reminder of the power of statistics to help us understand and interpret data. By understanding normal distributions, we can better understand the world around us.

_{Tags Normal Distributions , Probability Distributions , Continuous vs. Discrete}