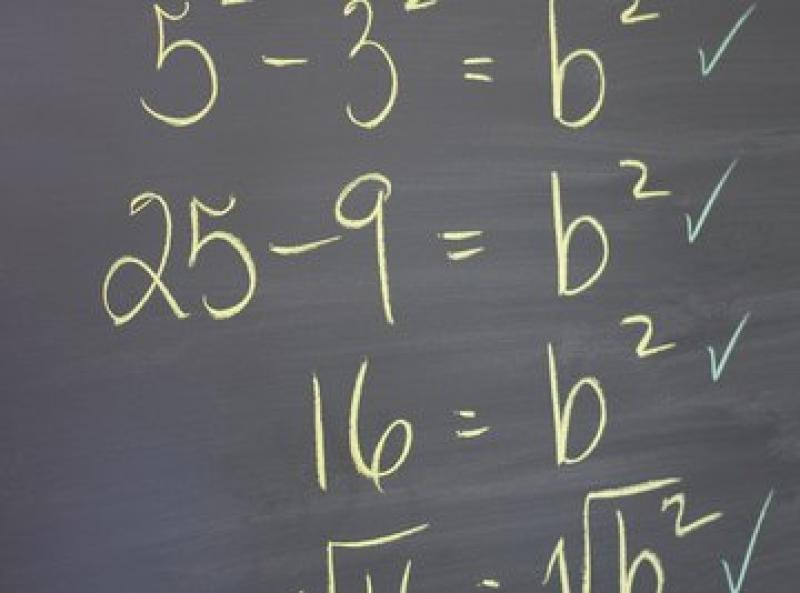Easy Steps to Learn Algebra: A Beginner's Guide

_{February 24, 2024 by JoyAnswer.org, Category : Education}

How to learn algebra in Easy Steps? Dive into the world of algebra with confidence using this beginner-friendly guide. Discover simplified steps and strategies to grasp algebraic concepts quickly and effectively.

How to learn algebra in Easy Steps?

Learning algebra can seem daunting at first, but with a systematic approach and practice, it can become more manageable. Here's a beginner's guide with easy steps to learn algebra:

Understand the Basics of Arithmetic: Before diving into algebra, make sure you have a solid understanding of basic arithmetic operations such as addition, subtraction, multiplication, and division. Familiarize yourself with properties of numbers, order of operations, and working with fractions and decimals.
Learn the Language of Algebra: Familiarize yourself with algebraic symbols and notation. Understand terms such as variables (usually represented by letters), constants, coefficients, and expressions. Learn how to translate word problems into algebraic expressions or equations.
Master Fundamental Concepts: Start with the fundamental concepts of algebra, such as:
- Solving equations: Learn to solve equations involving one variable by isolating the variable.
- Simplifying expressions: Practice simplifying algebraic expressions by combining like terms and using the distributive property.
- Understanding inequalities: Learn to solve and graph inequalities on a number line.
- Working with exponents and radicals: Understand the rules of exponents and how to simplify expressions involving exponents and radicals.
Practice Problem-Solving: Algebra is best learned through practice. Work on a variety of problems to reinforce concepts and improve problem-solving skills. Start with simple problems and gradually increase the complexity as you become more comfortable with the material.
Use Resources and Tools: Take advantage of resources available to help you learn algebra, such as textbooks, online tutorials, video lectures, and practice problems. Many websites and apps offer interactive lessons and quizzes to reinforce learning.
Seek Clarification: Don't hesitate to seek clarification from teachers, tutors, or classmates if you encounter difficulties understanding a concept or solving a problem. Algebra builds upon itself, so it's important to address any gaps in understanding early on.
Apply Algebra to Real-World Problems: Practice applying algebraic concepts to real-world situations. This can help you see the practical relevance of algebra and enhance your problem-solving skills.
Stay Organized and Review Regularly: Keep your notes and practice problems organized. Review previously learned concepts regularly to reinforce retention and build upon your knowledge.
Be Patient and Persistent: Learning algebra takes time and effort, so be patient with yourself and stay persistent. Don't get discouraged by challenges or setbacks. With consistent practice and perseverance, you can master algebra.

By following these easy steps and practicing regularly, you can build a strong foundation in algebra and develop the skills needed for more advanced mathematical concepts.

Unveiling the World of Algebra: Concepts, Strategies, and Resources

Algebra, the language of mathematics, forms the foundation for solving various mathematical problems. Here's a breakdown of its fundamental concepts, problem-solving approach, and helpful resources:

1. Foundational Concepts in Algebra:

Variables: Represented by letters (e.g., x, y, z), variables stand for unknown quantities.
Expressions: Combinations of numbers, variables, and operations (addition, subtraction, multiplication, division, exponents).
Equations: Statements expressing equality between two expressions. For example, 2x + 3 = 11.
Inequalities: Statements comparing two expressions using symbols like < (less than), > (greater than), ≤ (less than or equal to), and ≥ (greater than or equal to).
Functions: Relationships between variables where one variable's value (independent variable) determines the other variable's value (dependent variable).

2. Step-by-Step Approach to Solving Algebraic Equations:

Identify the equation: Clearly understand the given equation and what you need to solve for (usually the unknown variable).
Isolate the variable: Apply different algebraic operations (adding, subtracting, multiplying, dividing) to manipulate the equation and move the variable to one side by itself.
Simplify: Combine like terms (e.g., combine all x terms) and ensure the equation is in its simplest form.
Check for extraneous solutions: Substitute the obtained solution back into the original equation and verify that it holds true (not all manipulations, like dividing by zero, are always valid).

3. Resources for Mastering Algebra Concepts:

Textbooks and Online Courses: Utilize a dedicated algebra textbook or online course that provides clear explanations, examples, and practice problems.
Khan Academy: Offers free, high-quality video tutorials, practice exercises, and assessments covering various algebra topics.
Mathway: An online tool that provides step-by-step explanations for solving specific algebra problems (use responsibly to understand the steps, not solely rely on answers).
Tutoring: Consider enlisting the help of a qualified tutor who can personalize learning and address specific challenges.

Remember, practice is key to mastering algebra. Regularly work through practice problems, seek help when needed, and don't hesitate to ask questions. With dedication and the right resources, you can unlock the world of algebra and its numerous applications in mathematics and various other fields.