Altitude of a Right Triangle: Defining the Geometric Height

_{November 15, 2023 by JoyAnswer.org, Category : Mathematics}

What is the altitude of a right triangle? Explore the concept of the altitude of a right triangle, defining its geometric height. This article provides insights into the calculation and significance of the altitude in a right triangle.

Table of Contents

What is the altitude of a right triangle?

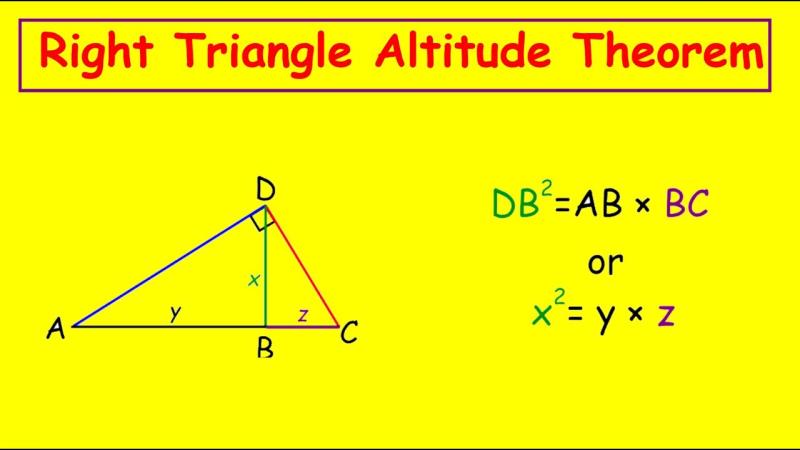
In geometry, the altitude of a right triangle is a line segment from one vertex of the triangle to the hypotenuse (the side opposite the right angle), forming a right angle with the hypotenuse. This line segment is often referred to as the "height" or "altitude" of the right triangle.

The altitude divides the right triangle into two smaller right triangles, each similar to the original right triangle. The altitude is crucial for several geometric properties and formulas associated with right triangles.

Here are some key points about the altitude of a right triangle:

Perpendicularity: The altitude is always perpendicular to the hypotenuse. This means that it forms a right angle with the hypotenuse.
Length: The length of the altitude can be determined using similar triangles and the properties of right triangles. The altitude divides the original right triangle into two smaller right triangles, and you can use the Pythagorean Theorem or other trigonometric ratios to find its length.
Area of the Right Triangle: The area of a right triangle can be calculated using the formula: $\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$ . In the context of a right triangle, the altitude is often considered the height.
Similarity: The three resulting triangles (the original right triangle and the two smaller right triangles formed by the altitude) are similar to each other. This similarity is a consequence of the angle-angle-angle (AAA) similarity criterion.

The altitude is a fundamental concept in geometry, providing a geometric height within a right triangle and facilitating the exploration of relationships between the sides and angles of the triangle.

Sure, here is an explanation of what an altitude of a right triangle is and how to calculate it:

Triangle height: What is the altitude of a right triangle?

The altitude of a right triangle is the perpendicular line segment drawn from a vertex to the opposite side of the triangle. In a right triangle, there are three altitudes, each corresponding to a different vertex. The altitude that is drawn to the hypotenuse is called the "altitude on the hypotenuse."

Defining and calculating the altitude of a right triangle in geometric terms

The altitude of a right triangle divides the triangle into two smaller right triangles, each of which is similar to the original triangle. This property, known as the "similar triangles" property, allows us to calculate the altitude of a right triangle using the following formula:

altitude = (base * height) / hypotenuse

where:

altitude is the length of the altitude we are trying to calculate
base is the length of the leg that is perpendicular to the altitude
height is the length of the other leg
hypotenuse is the length of the longest side of the triangle (opposite the right angle)

Tips for students and learners in applying geometric principles to right triangles

Here are some tips for students and learners in applying geometric principles to right triangles:

Familiarize yourself with the basic properties of right triangles: This includes understanding the concepts of the right angle, hypotenuse, base, and height.
Draw diagrams: When solving problems involving right triangles, it is often helpful to draw a diagram of the triangle to visualize the relationships between the sides and angles.
Label the sides and angles: Clearly label the sides and angles of the triangle to avoid confusion and ensure you are using the correct values in your calculations.
Learn and apply the Pythagorean theorem: The Pythagorean theorem is a fundamental tool for solving right triangle problems. It states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Practice with a variety of problems: Regularly practice solving right triangle problems to solidify your understanding of the concepts and improve your problem-solving skills.