The Unseen Language of Structure
Symbol languages are systems of communication that rely on specific, unambiguous symbols to convey complex ideas. From ancient cave paintings to modern programming code, they form the bedrock of logic, mathematics, and computing, enabling precision where natural language falls short. This exploration delves into their origins, evolution, and profound impact on our world.
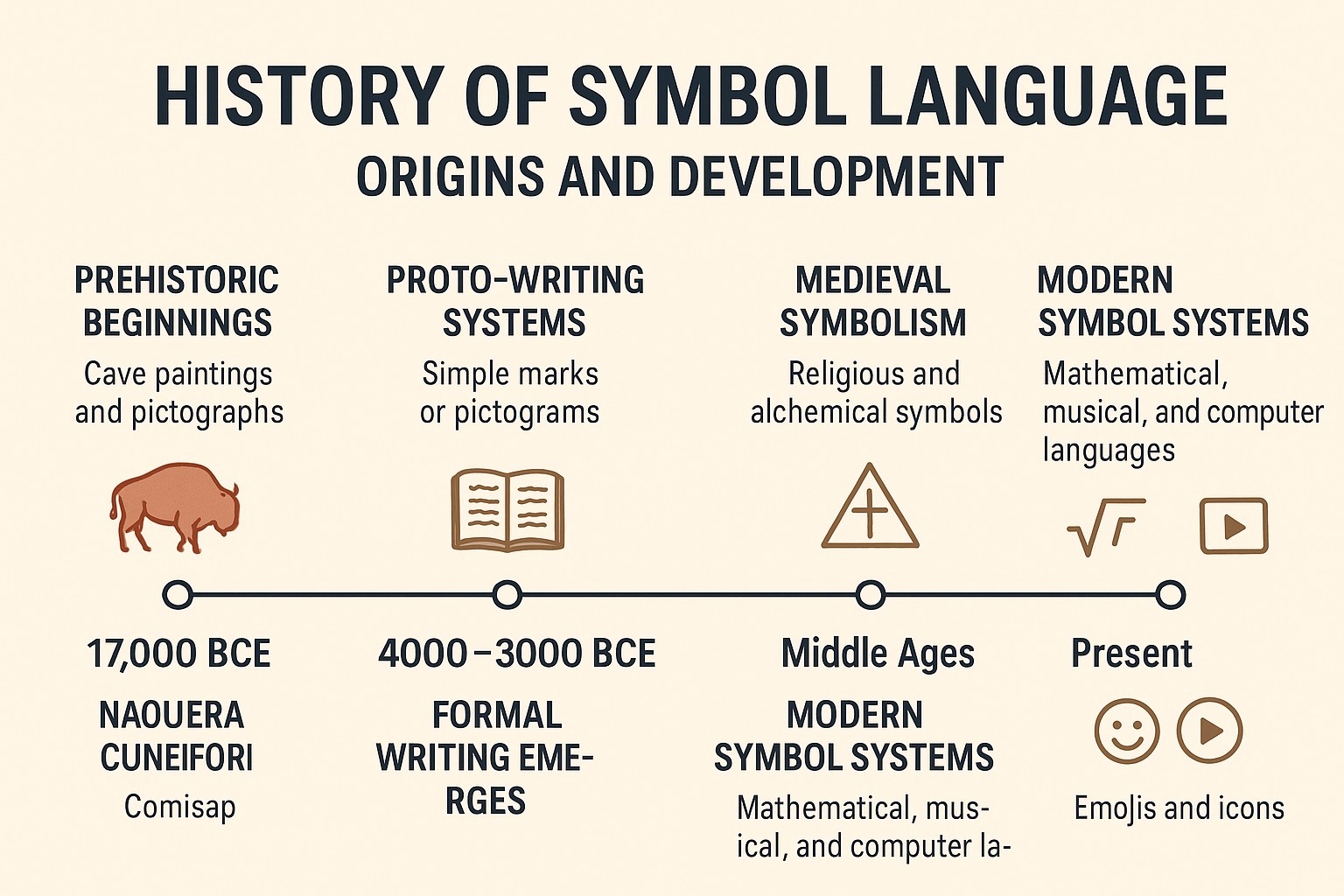
An Evolving Timeline
Follow the journey of symbolic representation through history. Click on any period to learn more.
Symbol vs. Natural Language
Symbol languages are designed for precision, while natural languages thrive on nuance and flexibility. This section highlights their fundamental differences across key characteristics.
Precision & Ambiguity
Symbol: Each symbol has one, and only one, meaning within its system. `x = 5` is absolute.
Natural: Words can have multiple meanings. The word "set" can be a verb, noun, or adjective.
Rules & Grammar
Symbol: Governed by strict, formal rules (syntax). A missing semicolon can break an entire program.
Natural: Grammar rules exist but are flexible and evolve. Slang and new expressions are common.
Context
Symbol: Generally context-independent. The meaning of `+` in math is consistent.
Natural: Heavily context-dependent. "It's cool" can refer to temperature or approval.
Expressiveness
Symbol: Limited to its defined domain (e.g., logic, math). Cannot express emotion.
Natural: Can express a vast range of abstract concepts, emotions, and subtleties.
Purpose
Symbol: Designed for formal reasoning, calculation, and instruction (e.g., proofs, algorithms).
Natural: Evolved for social communication, storytelling, and daily interaction.
Learning
Symbol: Learned formally through deliberate study and practice.
Natural: Acquired intuitively through immersion from a young age.
Key Applications & Domains
Symbol languages are the engines of modern science and technology. The chart below shows their primary domains of influence. Click on a segment to explore its role in that field.
Mathematics & Logic
This is the historical foundation of formal symbol languages. They provide the tools for constructing rigorous proofs and expressing complex relationships with perfect clarity. Symbols for operators (+, ∫), relations (=, <), and quantifiers (∀, ∃) allow mathematicians to build vast, consistent logical systems.
Computer Science
Programming languages are symbol languages that instruct machines. From low-level assembly to high-level Python, they use a strict syntax of keywords, variables, and functions to create software. Data structures, algorithms, and even network protocols are all defined using formal symbolic systems.
Chemistry & Physics
Chemical formulas (H₂O, C₆H₁₂O₆) are a compact symbol language to describe the composition of molecules. In physics, equations like E=mc² use symbols to represent physical quantities and their relationships, allowing for precise calculation and prediction of natural phenomena.